Question 692374: Graph the following system of linear inequalities {5x-4y≥0
{5x+7y≥55
{5x-3y≤70
x,y≥0
Thanks for any help, I do not understand this at all.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! You have 5 inequalities.
Each has a boundary (such as  ) that is included, and can be graphed as a line.
The other (x,y) pairs that satisfy the inequality are represented by all the points to one side of that graphed line.
You can use a convenient test point that is not on the line to see which side is in the solution.
You could graph all those inequalities separately, and find what parts of the x-y plane are common to all those graphs.
However, the points that satisfy all the inequalities may be part of a polygon limited by all those boundary lines.
The points where the boundary lines intersect could be the vertices of such a polygon and finding those points may be a better strategy.
THE EASY CONSTRAINTS:
 is graphed as the y-axis (the line with  ) and all the points to the right of the y-axis (all have  ).
 is graphed as the x-axis (the line with  ) and all the points above the x-axis (all have  ).
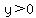Those 2 constraints tell us we are limited to the first quadrant.
THE INTERSECTION POINTS:
 -->  -->  -->  gives point A(56,70)
AND
 -->  -->  -->  -->  gives point B(4,5)
Those 2 points can be used to graph boundary line (line AB)
 -->  -->  gives point C(11,0)
Point (11,0) plus previously found point (4,5) can be used to graph boundary line  (line BC)
 -->  -->  gives point D(14,0)
Point (14,0) plus previously found point (56,70) can be used to graph boundary line  (line DA)
All of the above, along with test point P(10,10), can be graphed as
 Substituted, P's coordinates satisfy all the inequalities.
All the points on the same side of all boundary lines as point P are solutions.
The solution to the system is the quadrilateral ABCD, including its boundaries.
|
|
|
