Question 692098: Graph the system of equations. Then determine whether the system has "no solution" , "one solution", or "infinite solutions". If the system ha one solution name it.
Y= -1/2x + 3
Y= 2x - 2
(it shows just a plain graph)
I know it's "y= m(x) + b" but idk if I should use m = y2 - y1 over x2 - x1 I'm really confused.
Answer by ReadingBoosters(3246)   (Show Source):
You can put this solution on YOUR website! You are given the equation for both lines in the slope-intercept form(y=mx+b).
...
You can determine the solution to the system of equations algebraically and graphically.
...
To solve it graphically, you will graph each line and the solution is where the lines intersect.
...
Just by looking at the equations, you can tell that not only will they intersect, but the lines are perpendicular.
Perpendicular lines have negative inverse/reciprocal slope.
In the first line y=-1/2x + 3, the slope is  .
In the second line y= 2x - 2, the slope is 2.
is the negative reciprocal of 2
...
To graph a line, find the x and y intercept and draw a line through them.
the y intercept is b in the y=mx+b format
the x intercept is x when y is 0
...
For y = x+3
y intercept is 3, so plot (0, 3)
x intercept is found by:
0 = x + 3
-3 = x
-3(-2) =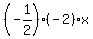 
6 = x, so plot (6, 0)
Then draw a line through the intercepts, so that it looks like:
...
For y = 2x - 2
y intercept is -2, so plot (0, -2)
x intercept is found by
01 = 2x - 2
2 = 2x
1 = x, so plot (1, 0)
Then draw a line through the intercepts and your graph should look like:
...
The "one solution" to the system is the point where they intercept,
( ,)
....
Algebraically, set the two equations equal to each other and solve for x
 ==> multiply both sides by 2
-1x + 6 = 4x - 4
6 + 4 = 4x + x
10 = 5x
x=2
...
Plug in x into either equation and solve for y
y = 2(2) - 2 = 4-2
y = 2
...
Confirmed, the solution/point of intersection is (2,2)
………………………
Have more math questions? Get them all addressed at once.
HomeworkHelpers@ReadingBoosters.com
for quick, personalized coaching
www.MyHomeworkAnswers.com
--Reading Boosters
|
|
|
