SOLUTION: Could someone please help me with this. Could someone show me how to sketch a function that is odd, one that is even, and one that is neither. Please and thank you!!!! One

Could someone please help me with this.
Could someone show me how to sketch a function that is odd, one that
is even, and one that is neither. 
Please and thank you!!!! 

Here are some that are EVEN.  What's on the left side of the y-axis 
is a mirror image of what is on the right side of the y-axis. They 
are said to be symmetrical with respect to the y-axis:
EVEN function:


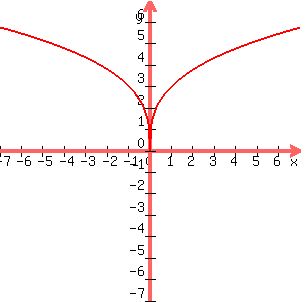EVEN function:


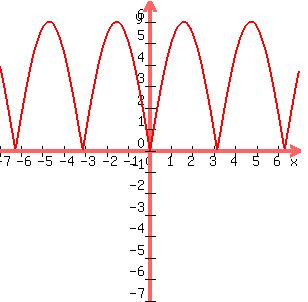EVEN function:


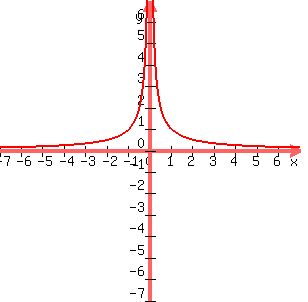EVEN function:


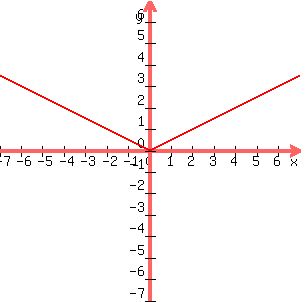Here are some that are odd.  What's on the left side of the y-axis is
upside down from what is on the right side of the y-axis.
They are said to be symmetical with respect to the ORIGIN.

Notice that an ODD function's graph looks exactly the same upside-down 
as it does right-side up.

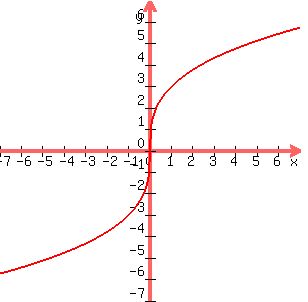ODD function:


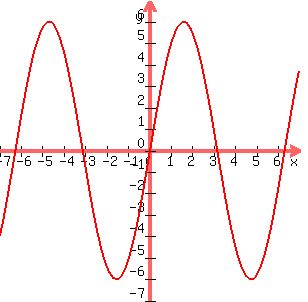ODD function:


ODD function:


ODD function:


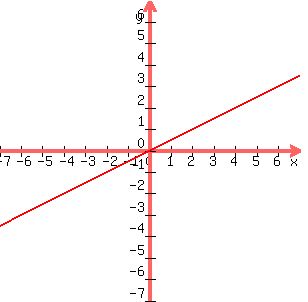Here is one that is neither.  

Neither ODD nor EVEN


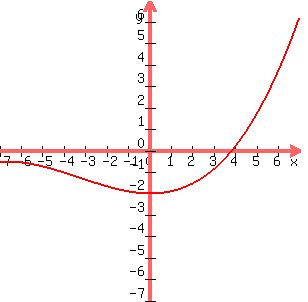Incidentally there is only one function that is both ODD and
EVEN, and that is the function whose graph is the x-axis. Its
equation is y = 0, graphed in purple below:



-------------------------------------------------------
One more that I am having trouble with is Graph y=2x^2-4x-6. Label 
all x-intercepts, y-intercepts, and the vertex. 

Here is the graph. You can find it by finding and plotting some points, 
or, what would be better, just wait until you get the points you are 
asked to find below. But here it is in advance:

Notice that it is neither an EVEN nor an ODD function.

To find the x-intercepts, replace y by 0 and solve for x:

y = 2x² - 4x - 6

0 = 2x² - 4x - 6

Divide every term by 2

0/2 = 2x²/2 - 4x/2 - 6/2

0 = x² - 2x - 3

Factor the right side:

0 = (x + 1`)(x - 3)

Set each factor = 0:

x + 1 = 0 gives x = -1
x - 3 = 0 gives x = 3

So the x-intercepts are (-1,0) and (3,0).
They are the two points where the graph 
crosses the x-axis:

To find the y-intercept, replace x by 0 and solve for y

y = 2x² - 4x - 6  
y = 2(0)² - 4(0) - 6
y = 0 - 0 - 6
y = -6

So the y-intercept is (0,-6). It is the point at which
the graph crosses the y-axis.

To find the vertex:

Factor the coefficient 2 out of the first two terms:

y = 2(x² - 2x) - 6

Complete the square by 
(1) multiplying the coefficient of x, -2,  inside the parentheses
    by 1/2, ( -2·1/2 = -1,  then
(2) squaring this result, (-1)² = 1
(3) adding and subtracting this inside the parentheses:

y = 2(x² - 2x + 1 - 1) - 6

Change the parentheses to brackets since they will soon have to
hold parentheses inside:

y = 2[x² - 2x + 1 - 1] - 6

Factor the first three terms as (x-1)(x-1) inside the brackets:

y = 2[(x - 1)(x - 1) - 1] - 6

Write (x-1)(x-1) as (x-1)²

y = 2[(x - 1)² - 1] - 6

Remove the brackets, keeping the (x-1)² intact:

y = 2(x - 1)² - 2 - 6

Combine the -2 and the -6

y = 2(x - 1)² - 8

Compare that to

y = a(x - h)² + k

and see that a = 2, h = 1, k = -8

So the vertex is (h,k) = (1,-8).

The vertex is the very bottom point on this
graph.  (Sometimes it's the very top point,
It's always the "turning point")

Edwin