|
Question 643885: I accidentally put the wrong equation in my original question - I am so sorry!
The corrected equation is shown below. Thanks again.
I am trying to test an equation for symmetry. The equation is x^2 = y^3 + 4.
I am starting by trying to find the intercepts. I think I found the intercepts for x - (2,0), (-2,0). I am having trouble finding the intercepts for y.
I substitute 0 for X and get 0 + y^3 + 4. I convert that to y^3 = -4. I am not sure where to go from there. Can I get a cube root of four? Solving for y, would my answer be the cube root of four i? Does that mean there is no y intercept?
I've confused myself... Thanks for any help.
Found 2 solutions by AnlytcPhil, MathLover1:
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To test for symmetry about the x-axis,
Substitute -y in place of y and see if it is possible to
simplify the equation back to its original form. If this
is possible it is symmetrical with respect to the x-axis.
To test for symmetry about the y-axis,
Substitute -x in place of x and see if it is possible to
simplify the equation back to its original form. If this
is possible it is symmetrical with respect to the y-axis.
To test for symmetry about the origin,
Substitute -x in place of x and -y in place of y and see
if it is possible to simplify the equation back to its
original form. If this is possible it is symmetrical with
respect to the x-axis.
-------------------------------------
Let's test for symmetry about the x-axis
x² = y³ + 4
Substitute -y for y
x² = (-y)³ + 4
x² = -y³ + 4
That is not like the original and has one term with the opposite sign
as the corresponding term in the original, so it cannot
be made into the same equation as the original.
Therefore it is not symmetrical about the x axis.
-------------------------
Let's test for symmetry about the y-axis
x² = y³ + 4
Substitute -x for x
(-x)² = y³ + 4
x² = y³ + 4
That is the same as the original so it is
symmetrical with respect to the y-axis.
--------------------------
Let's test for symmetry about the origin
x² = y³ + 4
Substitute -s for x and -y for y
(-x)² = (-y)³ + 4
x² = -y³ + 4
That is not like the original and has one term with the opposite sign
as the corresponding term in the original, so it cannot
be made into the same equation as the original.
Therefore it is not symmetrical about the origin.
The graph is below, but I don't think you had to do that,
just test for symmetry.
Yes you can take the cube root (or any odd root) of any number.
y = ∛x²-4
We can see it is symmetrical with respect
to the y-axis, but not the x-axis or origin.
 Edwin
Edwin
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! three types of symmetry:
A graph is said to be symmetric about the  if whenever (a,b) is on the graph then so is (a,-b) . if whenever (a,b) is on the graph then so is (a,-b) .
A graph is said to be symmetric about the  if whenever (a,b) is on the graph then so is (-a,b). if whenever (a,b) is on the graph then so is (-a,b).
A graph is said to be symmetric about the 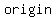 if whenever (a,b) is on the graph then so is (-a,-b). if whenever (a,b) is on the graph then so is (-a,-b).



follow this link to see your graph:
http://imageshack.us/photo/my-images/222/capture8302012103631pm.jpg/
now find 
 ........raise to power of three ........raise to power of three




 or or 
A graph is symmetric about the  if whenever (a,b)=(2,0) is on the graph then so is (-a,b)=(-2,0). if whenever (a,b)=(2,0) is on the graph then so is (-a,b)=(-2,0).
now find 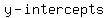 ...set ...set 


 ...use cube root calculator ...use cube root calculator
 ...so, ...so, 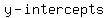 is at ( is at ( , ,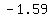 ) )
|
|
|
| |