I have found the horizontal asymptote to be y=0
So you know that on the far right and the far left the graph gets
closer and closer to the x-axis.
I have found the zero to be x=0
So you know that the graph crosses the x-axis where x is 0, which is
at the origin. So mark the origin:

I have found the vertical asymptote to be x=2 or x=-2
So draw those vertical lines. I'll draw them solid in green, but you
can draw them dotted.

I have also found the nature of Region 1,2,3 & 4
You have found that y is negative in region 1. So you know that
the graph is below the x-axis in region 1. And you know that
the graph must approach the x axis on the far left. You know that on
the right side of region 1, the graph must approach the vertical
asymptote x=-2. So you can sketch that part of the graph like this:
 You have found that y is positive in region 2. So you know that
the graph is above the x-axis in region 2. And you know that
the graph must approach the vertical asymptote x=-2 on the far left
of region 2. You also know that the graph must connect to the origin
on the right of region 2. So you can sketch that part of the graph
like this:
You have found that y is positive in region 2. So you know that
the graph is above the x-axis in region 2. And you know that
the graph must approach the vertical asymptote x=-2 on the far left
of region 2. You also know that the graph must connect to the origin
on the right of region 2. So you can sketch that part of the graph
like this:
 You have found that y is negative in region 3. So you know that
the graph is below the x-axis in region 3. And you know that
the graph in region 3 starts at the origin and goes down
and must approach the vertical asymptote x=2 on the right of
region 3. So you can sketch that part of the graph like this:
You have found that y is negative in region 3. So you know that
the graph is below the x-axis in region 3. And you know that
the graph in region 3 starts at the origin and goes down
and must approach the vertical asymptote x=2 on the right of
region 3. So you can sketch that part of the graph like this:
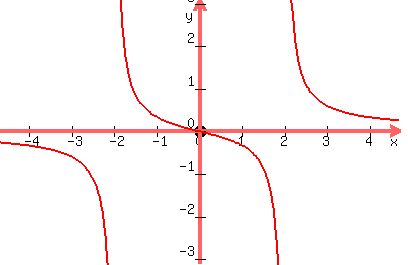
 You have found that y is positive in region 4. So you know that
the graph is above the x-axis in region 4. And you know that
the graph must approach the x axis on the far right. And on the
left side of region 4 of the graph must approach the vertical
asymptote x=2. So you can sketch that last part of the graph
like this:
You have found that y is positive in region 4. So you know that
the graph is above the x-axis in region 4. And you know that
the graph must approach the x axis on the far right. And on the
left side of region 4 of the graph must approach the vertical
asymptote x=2. So you can sketch that last part of the graph
like this:
 Edwin
Edwin