Question 557742: Using the distance formula and the Pythagorean theorem, determine whether the following set of points could be vertices of a right triangle: (-4,5), (6,1) and (-8, -5). I tried using the distance formula and the Pythagorean theorem. I figured out was what the length of the hypotenuse is (I think), but I don't know what to do next. I am confused by the fact that I have 3 sets of numbers (or 6 total numbers) and the formula only needs 2 sets (4 total).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the points of your triangle are:
(-4,5)
(6,1)
(-8,-5)
if the vertices of this triangle are the vertices of a right triangle, then one of the vertices must have it's sides perpendicular to each other.
you basically need to find the equations for the lines that form the triangle and then determine if any of them are perpendicular to any of the others.
to determine whether they are perpendicular, you need to determine if the slope of any one of the lines is perpendicular to the slope of any of the other lines.
you probably don't even need the equation of the lines.
all you really need is the slope of the lines, since that is what will allow you to determine whether the lines are perpendicular to each other or not.
the pairs of points that you want to examine for their slope are:
(-4,5) and (6,1)
(-4,5) and (-8,-5)
(6,1) and (-8,-5)
these pairs of points are the endpoints of the sides of your triangle.
the formula for slope is (y1-y2) / (x1-x2)
for the first pair of points, you define:
(-4,5) as (x1,y1)
(6,1) as (x2,y2)
applying the formula, you get:
(y1-y2)/(x1-x2) = (1-5)/(6-(-4)) which becomes -4/10
that's the slope of your first lline.
for the second pair of poinbts, you define:
(-4,5) as (x1,y1)
(-8,-5) as (x2,y2)
applying the formula, you get:
(y1-y2)/(x1-x2) = (-5-5)/(-8-(-4)) which becomes -10/-4 which becomes 10/4
you could apply the formula to the third pair of points, but it doesn't look like you need to because:
-4/10 is the negative reciprocal of 10/4.
this means that your triangle is a right triangle because 2 of the sides are perpendicular to each other.
you can confirm this is true by looking at the graph of your triangle.
In order to do so, however, you would need to find the equation for each of the lines and solve for y in order to graph them.
i did that for you, and the equations i got are:
first line:
y = (-4/10)x + (34/10)
second line:
y = (10/4) + 15
third line:
y = (3/7)x - (11/7)
a graph of these equations shows the following:
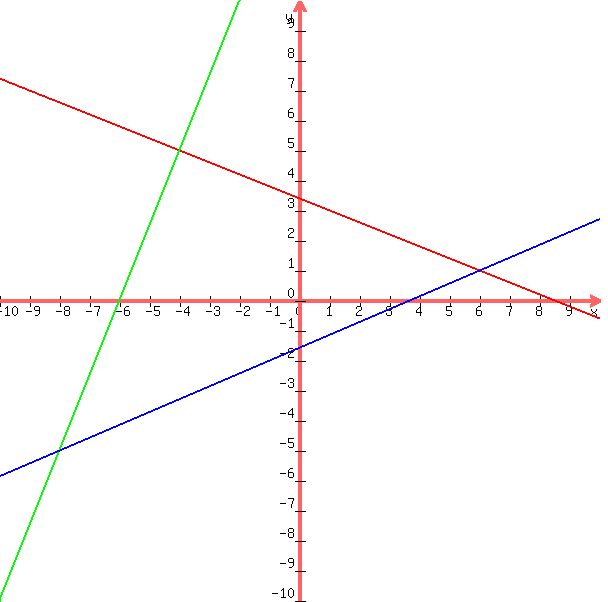
a picture of this graph with labels will show you more clearly the triangle, the equations of each of the lines, and the angle that is the right angle in this triangle.

|
|
|