|
Question 554427: How to solve the inequality -4(2x+7)<16?
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given to solve:
.
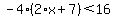
.
In general, you can work inequalities such as this one using the same rules as you would for equations with the exception that if you divide or multiply both sides by a negative quantity, the sign of the inequality will reverse direction.
.
So, let's begin by doing the distributed multiplication on the left side. Multiplying both terms inside the parentheses by -4 results in:
.
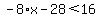
.
Next, let's get rid of the -28 on the left side by adding +28 to both sides. The -28 and the +28 will cancel each other on the left side and on the right side the +16 and the +28 total to +44. So the inequality is now:
.
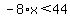
.
Just as we would do for an equation, we can solve for x by dividing both sides by -8. But remember the rule that if we divide or multiply both sides by a minus quantity, the direction of the inequality sign changes.
.
Dividing the -8x by -8 results in just x and dividing 44 by -8 gives 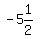 . And reversing the direction of the inequality sign due to the division by the MINUS 8 makes it change direction so it points to the right as shown: . And reversing the direction of the inequality sign due to the division by the MINUS 8 makes it change direction so it points to the right as shown:
.
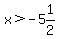
.
This tells us that the original inequality that we were given will only be true for values of x that are greater than 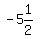 . On the number line, such values lie to the right of . On the number line, such values lie to the right of 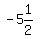 . .
.
Let's raise our confidence in that answer by taking the original inequality and substituting a value for x that is greater than 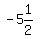 to see if it works. Let's try letting x equal -5: to see if it works. Let's try letting x equal -5:
.
Start with:
.
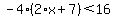
.
Replace x by -5 to get:
.
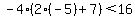
.
Inside the parentheses the 2 multiplies the -5 to give -10 and the +7 adds to the -10 to result in -3. This leads to:
.

.
and then:
.
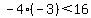
.
Multiplying the -4 times the -3 gives +12 so when x equals -5, the inequality becomes:
.
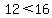
.
That certainly is true ... 12 is less than 16. So for a value of x that is slightly greater than 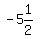 the original inequality that we were given is true. the original inequality that we were given is true.
.
For practice, why don't you see what happens when x is replaced by something slightly less than 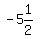 meaning that it lies slightly to the left of meaning that it lies slightly to the left of 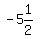 on the number line. If you try letting x equal -6 in the original inequality, you should get: on the number line. If you try letting x equal -6 in the original inequality, you should get:
.
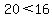
.
But that is not true. +20 is greater than +16. So x cannot be -6 and still have the original inequality be true. Somewhere between x equals -5 and x equals -6, the value of x will make the inequality go from being true to being untrue. That helps to give us confidence that our answer is correct. x must be greater than some value between -5 and -6.
.
For more practice, why don't you try letting x be exactly 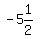 and see what happens when you substitute that value for x into the original inequality? You should get: and see what happens when you substitute that value for x into the original inequality? You should get:
.

.
That is not true. +16 is equal to, not less than +16. This tells you that, on the number line you must go a little to the right of 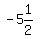 to make the original inequality be true. This establishes that our answer is correct. Namely, it must be that: to make the original inequality be true. This establishes that our answer is correct. Namely, it must be that:
.
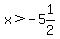
.
Hope this helps you to understand the problem a little better.
|
|
|
| |