6x² - 2xy + y³ = 9
Find the derivative implicitly term by term:
12x - 2(x + y) + 3y²
+ y) + 3y² = 0
Solve for
= 0
Solve for  12x - 2x
12x - 2x - 2y + 3y²
- 2y + 3y² = 0
Isolate the terms in
= 0
Isolate the terms in  -2x
-2x + 3y²
+ 3y² = -12x + 2y
= -12x + 2y
 (-2x + 3y²) = -12x + 2y
(-2x + 3y²) = -12x + 2y
 =
=  Write the positive terms first
Write the positive terms first
 =
= 
 =
= 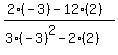 =
= 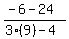 =
=  =
= 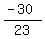 =
= 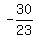 Finding the tangent line is the algebra problem of finding the equation
of the line through the point (2,-3) with a slope of
Finding the tangent line is the algebra problem of finding the equation
of the line through the point (2,-3) with a slope of 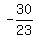 The equation of the tangent line at (2,-3) is
y =
The equation of the tangent line at (2,-3) is
y = 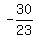 x -
x - 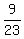 Finding the normal line is the algebra problem of finding the equation
of the line through the point (2,-3) with a slope of
Finding the normal line is the algebra problem of finding the equation
of the line through the point (2,-3) with a slope of 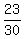 The equation of the normal line at (2,-3) is
y =
The equation of the normal line at (2,-3) is
y = 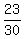 x -
x - 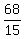 Edwin
Edwin