Question 55044: f(x)=x^2-3 How do I solve this problem I have tried several times and I do not think I have the right answer
Found 2 solutions by Nate, Hook:
Answer by Nate(3500)   (Show Source):
Answer by Hook(36) (Show Source):
You can put this solution on YOUR website! You can't "solve" this, per se. I think the problem asked you to "graph"  .
This is a parabola. Here's what I do for graphing parabolae:
I Find the real zeros (if any)
II find the apex
III figure out which way it opens
IV find any additional points
Ok...on to the work
I Find the real zeros.
I'll make y=0 to see where the graph crosses the x-axis
adding three to both sides gives
and if I take the square root, I get
and
(for the record,  is close to 1.71...not easily graphable.
Ok...not much use.
II Find the apex.
the formula for the x-coordinate of the apex of a parabola is  For us,  so the x-coordinate must also be zero. Let's plug that in and see what we get:
The apex is at (0,-3)
III which way does it open:
 , so it must open upwards
IV Plug in points.
At this point, we know we have an upward-opening parabola with an apex of (0,-3)
Let's plug in a few points to get some points to draw. I'll pick a couple on each side of the apex.
I'll use x = [-4,-2,2,4] as a set of points to graph
by plugging those into the equation, I get y = [13, 1, 1, 13]
So, we've come up with five points (really, you only need three..the apex and one on each side of the apex). That should be enough to graph this parabola.
We've got (x,y) = (-4,13),(-2,1), (0,-3), (2,1), (4,13)
Plot those points, play connect the dots, and you get this:
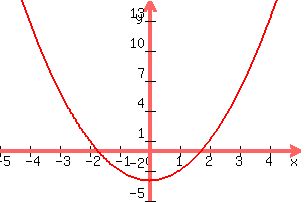
Here's probably an easier way to graph this:
Realize that is merely a "standard" parabola ( shifted down three units. Put a dot on the apex (0,-3). Go right one unit and up one unit (1,-2) and put a dot there. Go back to the apex. Go right two units and up four units to (2, 1). Repeat for the left side. That should be all ya need.
|
|
|
