Question 54478: Given a circle: (x-4)^2 + (y+5)^2 = 5, find the equation of the line (in slope-intercept form) that is tangent to this circle at the point (3,-7). Hint: use the fact that a tangent line is perpendicular to the radius of the circle at the point where they meet.
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The problem tells you that (3,-7) is a point on the circle, but is it really?
Check this by filling in 3 for x and -7 for y
(x-4)^2 + (y+5)^2 = 5
(3-4)^2 + (-7+5)^2 = 5
(-1)^2 + (-2)^2 = 5
1 + 4 = 5
So (3,-7) really is on the circle
Where is the center of the circle?
The equation is in the form
(x - a)^2 + (y - b)^2 = r^2
where (a,b) is the center, and r is the length of the radius
So the center is (4,-5) and r^2 = 5, so r = 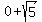
Now you have the endpoints of the line, so use

where


and


The key is to get this equation in the form 
then the slope of any line perpendicular to it will have the
slope 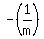


multiply both sides by (x - 3)


The slope m = 2, so the slope of a line perpendicular to this line
will have slope 
This is the slope of the tangent line at (3,-7), so you can write


multiply both sides by 2

multiply both sides by x-3



Does this line go through (3,-7) ? Check it




OK
|
|
|