Question 506571: A bus leaves town P for another town Q at time 1300 and travels at 60 km/h. A car traveling at 80 km/h leaves P by the same route an hour later. Using a horizontal scale of 2 cm for 1 hour and a vertical scale of 2 cm for 100 km, draw the distance-time graphs and find, graphically, when the car overtakes the bus.
If the bus arrives at Q half an hour later than the car, find, graphically or otherwise, the distance from P to Q.
*Please explain how do I draw the graph, since distances are not given and please answer as soon as possible :) =)
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bus leaves town P for another town Q at time 1300 and travels at 60 km/h.
A car traveling at 80 km/h leaves P by the same route an hour later.
Using a horizontal scale of 2 cm for 1 hour and a vertical scale of 2 cm for 100 km, draw the distance-time graphs and find, graphically, when the car overtakes the bus.
:
Write a slope intercept equation for the bus and the car
x = time, y = dist
y = 60x; bus equation (Red)
and
y = 80(x-1); (Green)
:
Plot a graph with these two equations, find y when x=2, x=6 for both equations
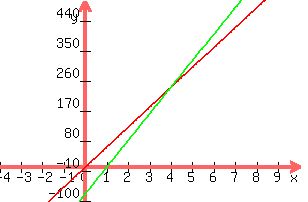
note the point of intersection, x=4 hrs, y=240 km, the car overtakes the bus
:
:
If the bus arrives at Q half an hour later than the car, find, graphically or otherwise, the distance from P to Q.
:
Let's use "otherwise", write a time equation, time = dist/speed
let d = dist from intersect to Q (240 km from P)
:
Bus time - Car time = .5 (half hour)
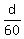 - -  = .5 = .5
multiply by 240, results
4d - 3d = 240(.5)
d = 120 km from the point of intersection which is 240 km from P, therefore
120 + 240 = 360 km from P to Q
:
:
:
We can confirm this, the travel time of the Bus was 1.5 hrs longer than the Car
(Car started 1 hr later and arrived half hour sooner), find the times
360/60 = 6 hr, bus time
360/80 = 4.5 hr, car time
|
|
|