|
Question 485713: |h|>6
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are asked to solve for the values that h can have to satisfy the inequality:
.
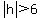
.
Your book or your teacher may have a different way of doing absolute value problems such as this one, but I'll show you a way that I like to do these.
.
You will solve two separate inequalities. One inequality will be done by first eliminating the absolute value bars and putting a plus sign + in front of the whole quantity that was inside these absolute value bars. The second inequality will also be done by first eliminating the absolute value bars, but then you put a minus sign - in front of the whole quantity that was inside these absolute value bars.
.
One other thing to remember. If you multiply or divide both sides of an inequality by a negative quantity, you need to reverse the direction of the inequality.
.
This may sound a little complex, but it's really pretty easy to do.
.
Start with the inequality you were given to solve for h:
.
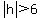
.
Eliminate the absolute value bars and assume that h has a plus sign in front of it:
.
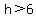
.
That's the first answer. h can be any value greater than +6 and that means that h can lie to the right of +6 on the number line.
.
Now let's solve the second inequality. Again start with the inequality you were given to solve for h:
.
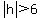
.
Eliminate the absolute value bars and this time assume that h has a minus sign in front of it:
.
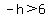
.
But we need to solve for +h. In order to do that we can multiply both sides of the inequality by -1. Remember the rule, however. When you multiply both sides by a negative 1, you also have to reverse the direction of the inequality sign.
.
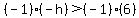
.
The multiplication results in a plus h on the left side and a minus 6 on the right side as follows:
.

.
and because of the multiplication of both sides by a negative number, we reverse the direction of the inequality sign and get:
.
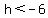
.
This means that h can also be any number less than -6 (or any number that is to the left of -6 on the number line).
.
In summary, the answer to this inequality problem is that h must either be greater than +6 or it must be less than -6.
.
To help you a little further with using this method, let's work another quick example. Suppose the problem you are given is:
.
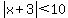
.
Very quickly, first eliminate the absolute value bars and put a plus in front of the quantity inside the bars to get:
.
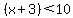
.
Since the parentheses are preceded by a presumed + sign, the parentheses can be removed without changing the signs of he terms within. This simplifies the inequality to:
.
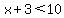
.
Subtract 3 from both sides. (NOTE: This negative quantity does not change the direction of the inequality sign because it is subtraction NOT multiplication or division.)
.

.
and the subtraction on both sides results in:
.
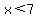
.
So one of the answers is that x must be less than 7 (or to the left of +7 on the number line).
.
Now for the second solution. Return to the original problem:
.
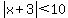
.
Eliminate the absolute value bars and put a negative sign in front of the entire quantity that was within the bars to get:
.
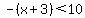
.
Remove the parentheses by changing the signs on each of the terms that they contain. This results in:
.

.
Add 3 to both sides:
.
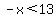
.
Multiply both sides by -1 to solve for positive x and don't forget to reverse the direction of the inequality sign. When you do those steps the resulting answer is:
.
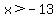
.
This means that x must be greater than -13 (or x is to the right of -13 on the number line).
.
Combining the two answers we have x must be smaller than +7, but it must be larger than -13. So the values that x can have are between -13 and +7.
.
I hope this example adds a little more explanation and provides you with a little more understanding on how to do absolute value problems. Please double check my work to ensure that I didn't make any dumb mistakes. It's too late and I probably should not be working math problems.
|
|
|
| |