Question 484807: I need help with inequalities problems, I don't know a thing!!!
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! THIS SIGN < means is less than..
This sign > means is greater than.
In each case, the sign opens towards the larger number.
For example, 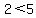 ("2 is less than 5"). Equivalently, ("2 is less than 5"). Equivalently,  } ("5 is greater than 2"). } ("5 is greater than 2").
These are the two senses of an 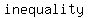 : < and > , : < and > ,
and you also might have ≤, "is less than or equal to" or ≥, "is greater than or equal to"
On the number line, 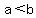 means: a falls to the left of means: a falls to the left of  . .
ex.:
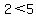
−1 < 2
a compound inequality:
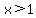 and x ≤ 5. and x ≤ 5.
It is a compound sentence whose conjunction is "and." It says that x takes on values that are greater than 1 and less than or equal to 5.
It is within that interval that x takes its values. The endpoint 1 is not included. x is definitely greater than 1; we indicate that by placing a parenthesis "(". The endpoint 5 is included; we indicate that by placing a bracket "]".
A continued inequality
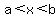
That is called a continued inequality. It means
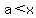 and and 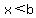
A continued inequality always implies the conjunction and. The sense is always < or ≤.
The continued inequality means:
x falls in the interval between a and b.
"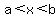 " illustrates that " illustrates that
Some theorems of inequalities
To prove a statement whose predicate is "is greater than," we must have a definition of "is greater than." We shall adopt the following. We shall define "a is greater than b" to mean: a − b is positive.
Algebraically:
 if and only if a − b > 0 if and only if a − b > 0
Theorem 1. We may add the same number to both sides of an inequality, and the sense will not change.
Theorem 1 as follows:

means
a − b > 0
upon adding and subtracting c :
a − b + c − c > 0
(a + c) − (b + c) > 0
Theorem 2. We may multiply both sides of an inequality by the same positive number, and the sense will not change.
If
a > b, and c > 0,
then
ca>cb.
For example:
4 > −5
If we now multiply both sides by 3, for example, then
12 > −15.
The sense does not change.
|
|
|