Question 47734This question is from textbook College Algebra
: Graph the function, not by plotting points, but by starting from the graph of y = e^x. State the domain, range, and asymptote.
y = 1- e^x
I tried graphing these on the computer but it won't take these exponents so I'm at a loss although I know that there is some shifting involved with the first constant.
Thank you so very much for this help!
This question is from textbook College Algebra
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! sketching graphs is one of the most important skills you can have in your arsenal in maths. Forget graphical calculators..they are rubbish in my honest opinion.
start with LEARNING the shape of  . I cannot draw it here, but look in your books. Learn its shape and the fact that it has no y-values and that when x=0, then y=1. . I cannot draw it here, but look in your books. Learn its shape and the fact that it has no y-values and that when x=0, then y=1.
Right, what about  . Adding a negative sign has the action of flipping the whole curve upside down, as if mirrored in the x-axis. . Adding a negative sign has the action of flipping the whole curve upside down, as if mirrored in the x-axis.
So we now have the same shaped curve but it exists completely under the x-axis now and goes through (0,-1).
Now, finally we have  which you can think of as y=1 + which you can think of as y=1 + 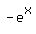 , so we have the -ve curve and we add a value of 1 to each point. This has the effect of moving the whole curve up by 1 unit, so the shape is unaltered and whereas we had the curve skimming along the x-axis for negative values of x, now we have the curve skimming along x=1 and then it moves down through (0,0) instead of (0,-1). , so we have the -ve curve and we add a value of 1 to each point. This has the effect of moving the whole curve up by 1 unit, so the shape is unaltered and whereas we had the curve skimming along the x-axis for negative values of x, now we have the curve skimming along x=1 and then it moves down through (0,0) instead of (0,-1).
Hope this makes sense.
jon.
|
|
|