Question 356772: find the vertex of the x and y coordinate, line of symmetry and maximum of f(x)
f(x)=-2x^2+2x+7
Found 2 solutions by CharlesG2, Edwin McCravy:
Answer by CharlesG2(834)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the vertex of the x and y coordinate, line of symmetry and maximum of f(x)
f(x)=-2x^2+2x+7
f(x) = -2x^2 + 2x + 7, this is of form f(x) = ax^2 + bx + c
a = -2, a < 0, so parabola opens downwards
f(x) = -2x^2 + 2x + 7 is standard form of the parabolic equation
converting to vertex form
f(x) = -2(x^2 - x) + 7
(-1/2)^2 = 1/4
-2 * 1/4 = -2/4 = -1/2
7 + 1/2 = 7 1/2 = 15/2
the above 3 lines were completing the square to get below line
f(x) = -2x^2 + 2x - 1/2 + 7 + 1/2 = -2(x^2 - x + 1/4) + 15/2
f(x) = -2(x - 1/2)^2 + 15/2
this is now in vertex form of f(x) = a(x - h)^2 + k, where (h,k) is vertex
vertex is (1/2,15/2)
axis of symmetry -> x = h = 1/2
maximum of f(x) since parabola opens downwards is k or 15/2
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the vertex of the x and y coordinate, line of symmetry and maximum of f(x)
f(x)=-2x^2+2x+7.
There are two methods, {1) completing the square using the memorized
standard form f(x) = ax²+b+c
and
(2) using the vertex formula that you have memorized.
-----------------------------------------
Method (1)
f(x) = -2x² + 2x + 7
Factor out -2 from the first two terms:
f(x) = -2(x² - x) + 7
To the side multiply the coefficient of x, which is -1, by  getting getting
 then squaring then squaring  getting getting 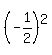 or or  . Then
adding that and subtracting that inside of the parentheses:
f(x) = -2(x² - x + . Then
adding that and subtracting that inside of the parentheses:
f(x) = -2(x² - x +  - -  ) + 7
Change the parentheses to brackets (so you can put parentheses inside):
f(x) = -2[x² - x + ) + 7
Change the parentheses to brackets (so you can put parentheses inside):
f(x) = -2[x² - x +  - -  ] + 7
Factor the first three terms inside the brackets:
f(x) = -2[(x - ] + 7
Factor the first three terms inside the brackets:
f(x) = -2[(x -  )(x - )(x -  ) - ) -  ] + 7
Since those factors in parentheses are the same we write them
as a perfect square:
f(x) = -2[(x - ] + 7
Since those factors in parentheses are the same we write them
as a perfect square:
f(x) = -2[(x -  )² - )² -  ] + 7
Now remove the brackets by using the distributive
principle. That is, we multiply the -2 by putting
it in front of the (x - ] + 7
Now remove the brackets by using the distributive
principle. That is, we multiply the -2 by putting
it in front of the (x -  )^2 and we multiply
the -2 also by the )^2 and we multiply
the -2 also by the  getting -1. So we have
f(x) = -2(x - getting -1. So we have
f(x) = -2(x -  )² + )² +  + 7
Then we combine the two terms on the right side and get
f(x) = -2(x - + 7
Then we combine the two terms on the right side and get
f(x) = -2(x -  )² + )² +  + +  f(x) = -2(x -
f(x) = -2(x -  )² + )² +  We recognize this as in the standard form we have memorized:
f(x) = a(x - h)² + k
we know that a = -2, h =
We recognize this as in the standard form we have memorized:
f(x) = a(x - h)² + k
we know that a = -2, h =  and k = and k =  So that the vertex is (h,k) or (
So that the vertex is (h,k) or ( , ,  )
----------------
Method (2), using the vertex formula we have memorized:
x-coordinate of vertex = )
----------------
Method (2), using the vertex formula we have memorized:
x-coordinate of vertex =  y-coordinate of vertex = what you get when you substitute the
x-coordinate for x in the equation and simplify.
f(x) = -2x² + 2x + 7
Compare to the general form we have memorized,
f(x) = ax² + bx + c
a = -2, b = 2, c = 7
x-coordinate of vertex =
y-coordinate of vertex = what you get when you substitute the
x-coordinate for x in the equation and simplify.
f(x) = -2x² + 2x + 7
Compare to the general form we have memorized,
f(x) = ax² + bx + c
a = -2, b = 2, c = 7
x-coordinate of vertex =  = = 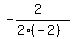 = =
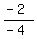 = =  y-coordinate of vertex = what we get when you substitute the
x-coordinate,
y-coordinate of vertex = what we get when you substitute the
x-coordinate,  for x in the equation and simplify:
f( for x in the equation and simplify:
f( ) = -2( ) = -2( ² + 2 ² + 2 + 7 = -2( + 7 = -2( ) + 1 + 7 = ) + 1 + 7 =  + 8 = + 8 =  + +  = =  so the vertex is the point V(
so the vertex is the point V( , ,  ).
-------
No that we have found the vertex by either of the above two methods,
we plot that point and draw a verticle line, the line of symmetry,
through it, like this line drawn in green: ).
-------
No that we have found the vertex by either of the above two methods,
we plot that point and draw a verticle line, the line of symmetry,
through it, like this line drawn in green:
 That green line of symmetry has the equation x =
That green line of symmetry has the equation x =  because
every point on that green line of symmetry has because
every point on that green line of symmetry has  as its
x-coordinate.
Now we can get some other points on that graph:
x| y
-----
-2|-5
-1| 3
0| 7
1| 7
2| 3 as its
x-coordinate.
Now we can get some other points on that graph:
x| y
-----
-2|-5
-1| 3
0| 7
1| 7
2| 3
 And the graph is
And the graph is
 The maximum value is the greatest y-value on the graph, which is the
y-coordinate of the vertex,
The maximum value is the greatest y-value on the graph, which is the
y-coordinate of the vertex,  Edwin
Edwin
|
|
|