Question 35477This question is from textbook algebra for college students
: Can you help me?
Find the vertices, the foci, and the equation of the asymptotes, and sketch the hyperbola:
4x^2 -y^2 -24x -4y +16 =0
This question is from textbook algebra for college students
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the vertices, the foci, and the equation of the asymptotes, and sketch the hyperbola:
4x^2 -y^2 -24x -4y +16 =0....IS YOUR PROBLEM .THE FOLLOWING EXAMPLE
y^2 - 4x^2 - 2y - 16x + 1 = 0 GIVEN BY ME
IS ALMOST SAME EXCEPT FOR A FEW CHANGES IN COEFFICIENTS.OUR OBJECTIVE IS TO HELP YOU IN UNDERSTANDING AND ENABLE YOU TO DO SUCH PROBLEMS ON YOUR OWN.THAT IS WHY WE ARE SUGGESTING YOU TO STUDY THIS EXAMPLE AND TRY TO DO YOUR PROBLEM BY YOUR SELF.YOUR QUESTIONS ARE
1.MANY EXAMPLES ARE GIVEN AND THEY ARE CONFUSING.
OK.I REMOVED THE OTHERS GIVEN FOR YOUR WIDER UNDERSTANDING/LEARNING.
2.WHAT IS ECCENTRICITY..
THIS IS A FUNDAMENTAL TERM/PROPERTY RELATED TO CONICS WHCH YOU SHOULD KNOW IF YOU HAVE STUDIED CONICS.IT IS THE RATIO OF THE DISTANCE OF A POINT ON THE CURVE FROM A GIVEN POINT CALLED FOCUS TO ITS DISTANCE FROM A GIVEN LINE
CALLED DIRECTRIX.
IF YOU HAVE NOT HEARD THESE TERMS SO FAR ,YOU NEED TO REVIEW THE TOPIC WITH YOUR TUTOR
BEFORE TRYING TO DO PROBLEMS.
3.SKETCHING AS A GRAPH.
ONCE YOU HAVE AN EQN.SKETCHING MEANS ,GIVE DIFFERENT VALUES TO X AND DETERMINE THE CORRESPONDING VALUES OF Y,TAKE A SUITABLE SCALE AND PLOT THEM ON A GRAPH.WHICH STEP YOU DO NOT KNOW HERE? FINDING Y FROM X VALUES FROM THE EQN?PLOTTING POINTS ON A GRAPH?THESE ARE AGAIN ELEMENTARY AND YOU HAVE TO REVIEW WITH YOUR TUTOR IF YOU DO NOT KNOW THESE THINGS.
THE REFERENCE POINTS LIKE VERTICES,CENTRE,AND LINES LIKE AXES,ASYMPTOTES WILL AID YOU
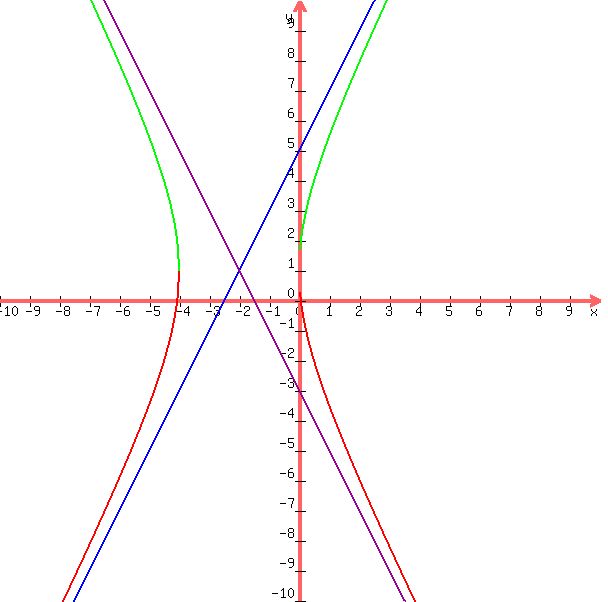
IN OUTLINING AND VERIFYING YOUR SKETCH.I HAD SHOWN YOU ALSO THE SHAPE OF THE CURVE IN THE ALGEBRA SITE AT THE END.
-------------------------------------------------------------------------------
HENCE TRY TO READ AND UNDERSTAND AND CHANGE THE CORRESPONDING NUMBERS TO GET YOUR ANSWER.COME BACK WITH SPECIFIC DIFFICULTIES IF ANY.
------------------------------------------
What is the vertices, foci, and slope of the asymptote for the hyperbola whose equation is, y^2 - 4x^2 - 2y - 16x + 1 = 0?
(Y^2-2*Y*1+1^2)-{(2X)^2+2*(2X)*4+4^2}-1^2+4^2+1=0
(Y-1)^2-(2X+4)^2=-16
4(X+2)^2-(Y-1)^2=16
{4(X+2)^2}/16-{(Y-1)^2}/16=1
(X+2)^2/2^2-(Y-1)^2/4^2=1...
COMPARING WITH STANDARD EQN.
(X-H)^2/A^2-(Y-K)^2/B^2=1....WE HAVE
CENTRE IS (H,K).....THAT IS (-2,1)
VERTICES ARE {(H-A),K} AND {(H+A),K}=(-2-2,1) AND (-2+2,1)=(-4,1) AND (0,1)
FOCI ARE {(H-AE),K} AND {(H+AE),K}...WHERE E IS
ECCENTRICITY =SQRT{(A^2+B^2)/A^2}=SQRT((4+16)/4)=SQRT(5)
SO FOCI ARE =(-2-2SQRT(5),1) AND (-2+2SQRT(5),1)
you can take this proposition as proved formula
the pair of asymptotes for a conic is given by the same equation as the conic except for the constant term which has to be found using the condition for the equation to represent a pair of straight lines.
HENCE EQN OF ASYMPTOTES IS GIVEN BY
y^2 - 4x^2 - 2y - 16x + K=0 , WHERE K IS DETERMINED using the condition for the equation to represent a pair of straight lines.
SINCE WE ARE TO FIND ONLY SLOPES ,WE NEED NOT DETERMINE THE CONSTANT BUT ASSUME THAT THIS EQN REPRESENTS A PAIR OF STRAIGHT LINES.SO
y^2 - 4x^2 - 2y - 16x + K=0 = (Y+2X+A)(Y-2X+B)
HENCE SLOPES ARE +2 AND -2
IF YOU WANT TO FIND EQN.OF ASYMPTOTES ,YOU CAN FIND K BY NOTING THAT THE ASYMPTOTES PASS THROUGH CENTRE THAT IS (-2,1)...SO...
1^2-4(-2)^2-2*1-16(-2)+K=0=1-16-2+32+K=15+K.....OR.....K=-15
HENCE EQN.OF ASYMPTOTES IS
y^2 - 4x^2 - 2y - 16x - 15=0..OR
Y+2X+3=0.....AND .....Y-2X-5=0
|
|
|