|
Question 347657: I have tried so many different things on this problem, thinking through why they would be what they are and I still got them wrong. Please help me understand. This is what I put for each in order, it is what I was convinced the answer was. (F,T,T,F,F,F,F) Why are any of these wrong?
(1 pt) Let the function f be defined by f(x) = {1}/{sqrt{1-x^2}}. Indicate whether the following statements are True (T) or False (F). You must get all answers correct in order to receive credit.
___1. f(x) is never positive.
___2. 1 is in the domain of f
___3. 0 is in the domain of f
___4. f(x) is never negative.
___5. All negative real numbers are in the domain of f
___6. f(x) is never zero.
___7. All positive real numbers are in the domain of f
Found 2 solutions by edjones, jim_thompson5910:
Answer by edjones(8007)   (Show Source):
You can put this solution on YOUR website! f(x)=1/sqrt(1-x^2)
.
2.
1-x^2>0 If it is zero then there is division by zero which is not allowed. If it is less than zero then the denominator is an imaginary number, also not allowed.
-x^2>-1
x^2<1
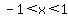
2 is F
.
The rest of your answers are correct.
.
Ed
Answer by jim_thompson5910(35256)  (Show Source):
|
|
|
| |
