Question 340408: I cannot differentiate between different forms of interval writing. What is interval writing and how do I know which brackets to use or what number goes where when I write out an answer? For example, 0 < 5-2x.
Found 2 solutions by Fombitz, solver91311:
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! When the inequality does not include an "=" sign, then the solution will not contain the interval endpoint, so then you would use a set of parentheses.
.
.
.
Example: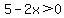 
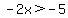
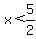
So the interval includes all numbers less than  but not .
In interval notation that would be,
( ,)
.
.
.
When the inequality does contain an "=" sign, then the solution would include the interval endpoint, so then you would use a bracket.
.
.
.
Example:
In interval notation,
(,]
.
.
.
And finally for a compound inequality,
Example: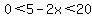
The one side you already solved,
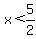
The other side is,
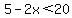
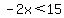
Putting those two together,
( ,)
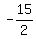Then look at all of the variations with the different inequality signs,
: (,)
 : [,)
 : [,]
 : (,]
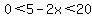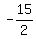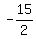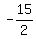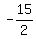Answer by solver91311(24713)  (Show Source):
|
|
|
