SOLUTION: 1. Show and explain the steps to solving the following systems of equations by graphing. For each problem tell the x- and y- intercepts of EACH line and the slope. a. 3x + 2y =

You can put this solution on YOUR website!
Next time please only put one problem in each submission.
1. a.

Solved by pluggable solver: DESCRIBE a linear EQUATION: slope, intercepts, etc

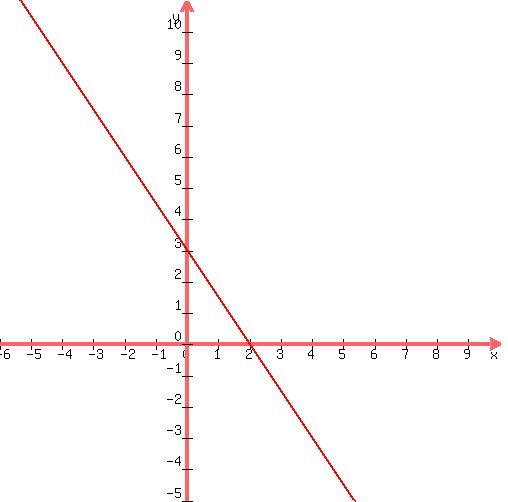
Equation describes a sloping line. For any equation ax+by+c = 0, slope is . X intercept is found by setting y to 0: ax+by=c becomes ax=c. that means that x = c/a. 6/3 = 2. Y intercept is found by setting x to 0: the equation becomes by=c, and therefore y = c/b. Y intercept is 6/2 = 3. Slope is -3/2 = -1.5. Equation in slope-intercept form: y=-1.5*x+3.

and

Solved by pluggable solver: DESCRIBE a linear EQUATION: slope, intercepts, etc

Equation describes a sloping line. For any equation ax+by+c = 0, slope is . X intercept is found by setting y to 0: ax+by=c becomes ax=c. that means that x = c/a. 8/4 = 2. Y intercept is found by setting x to 0: the equation becomes by=c, and therefore y = c/b. Y intercept is 8/-1 = -8. Slope is -4/-1 = 4. Equation in slope-intercept form: y=4*x+-8.

since in both equations the x intercept is 2, you can plug in 2 for x and solve for y:






You can also check your answer in a variety of ways.
1.b. Do in the same way as above (x=1.33333, y=1.33333)
1.c.Do in the same way as above (x=4, y=2)

2.a

-3(x + 5y = -15)
3x-2y=23
+(-3x-15y=45)



plug in y=-4 in one of the original equations.



We can check by pluging in x and y:



And in the other equation:



[b]Thus x=5 and y=-4[/b]
2.b. Same process as above (x=-5 and y=1.5)
2.c. Same process as above ( and )
Smiles,
lyra