SOLUTION: Will someone pleae show me how to Name the curve described by the following equation? (x+2)^2 + y^2 = 4 I'd like to know how to solve it manually with full working so that I can

Algebra ->  Graphs -> SOLUTION: Will someone pleae show me how to Name the curve described by the following equation? (x+2)^2 + y^2 = 4 I'd like to know how to solve it manually with full working so that I can       Log On


   

Question 316779: Will someone pleae show me how to Name the curve described by the following equation?
(x+2)^2 + y^2 = 4
I'd like to know how to solve it manually with full working so that I can also show the co-ordinates of the centre, and the radius of the shape.
Thanks, -Nick.
Answer by moshiz08(60) About Me  (Show Source):
You can put this solution on YOUR website!
Nick,
The curve described by the equation %28x%2B2%29%5E2+%2B+y%5E2+=+4 is a circle! It has a radius of 2, and its center is at the point (-2, 0).
First we must ask ourselves, what is a circle? A circle is the set of points of equal distance from the center point. The distance from the center to any point on the circle is the radius r. Let's say we have a general center point with coordinates (h, k).
So the distance from the center (h, k) to a point (x, y) on the circle is r. Do you remember the distance formula from geometry?
distance ( (a,b) , (c,d) ) = 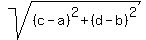sqrt%28+%28c-a%29%5E2+%2B+%28d-b%29%5E2+%29
If you don't recall this, plot a point (a, b) and another point (c, d) on a graph. Then form a right triangle. The base is parallel to the x-axis and has length |c-a|; and the height is parallel to the y-axis and has length |d-b|. Now use the Pythagorean Theorem to find the distance of the straight line connecting your two points (the hypotenuse of your right triangle).
Once we have established the distance formula, we can use our specific example. The distance from the center (h, k) to a point on the circle (x, y) is r.
distance( (h,k), (x,y) ) = +r+=+sqrt%28+%28x-h%29%5E2+%2B+%28y-k%29%5E2+%29+
Now square both sides and we get
+r%5E2+=+%28x-h%29%5E2+%2B+%28y-k%29%5E2+
In your particular question, r%5E2+=+4 so +r+=+2+, and clearly +h+=+-2+ and +k+=+0+, so the radius is 2 and the center is (-2, 0).
I hope this was helpful!
-Mo

P.S. The circle is part of a general class of curves called conic sections. I will summarize a couple of the other conic sections by giving you the equations, just for future reference.
Ellipse: +%28%28x-h%29%2Fa%29%5E2+%2B+%28%28y-k%29%2Fb%29%5E2+=+1+, where a and b are the major radius and minor radius (an ellipse is like an elongated circle so it doesn't have a constant radius). The center is still at the point (h,k).
Hyperbola: +%28%28x-h%29%2Fa%29%5E2+-+%28%28y-k%29%2Fb%29%5E2+=+1+ or +%28%28y-k%29%2Fa%29%5E2+-+%28%28x-h%29%2Fb%29%5E2+=+1+. Note that unlike the ellipse there is a minus sign.