Question 283642: The length of a rectangle is 3cm more than 2 times its width. If the area of the rectangle is 93cm^2, find the dimensions of the rectangle. Enter your answers in the blanks. Enter only the numeric values rounded to the nearest thousandth of centimeter Width=________cm, Length=_____________cm.
Answer by oberobic(2304)   (Show Source): (Show Source):
You can put this solution on YOUR website! L = length
W = width
A = area
A = L*W
.
L = 2W + 3
.
A = 93 cm^2
.
Substitute L = 2W+3 in the area equation to solve.
.
L*W = 93 cm^2
(2W +3) * W = 93
2W^2 + 3W = 93
2W^2 + 3W -93 = 0
.
This does not factor nicely, so you need to use the quadratic equation.
.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=753 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 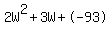 can be factored: can be factored:

Again, the answer is: 6.11021136700612, -7.61021136700612.
Here's your graph:
 |
.
This provides two solutions: W=6.11 and W=-7.61.
W cannot be negative, so the approximate value is W=6.11.
.
Substituting, W=6.11, we can find L.
L = 93/6.11
L = 15.22 cm
.
Checking, does the area = 93 cm^2?
(15.22)(6.11) = 92.9942 cm^2, which is close enough to 93.
Correct.
.
Checking, does L = 2W + 3?
2W = 2*6.11 = 12.22 cm
12.22 + 3 = 15.22 cm
Correct.
.
Answer:
L = 15.22 cm
W = 6.11 cm
.
Done.
|
|
|