SOLUTION: I have a question on transformations of graphs. I seem to have a little difficulty in finding the plots for graphs that are 'stretched' or 'shrunk'. For example: f(x)=x^2 is the ba

Algebra ->  Graphs -> SOLUTION: I have a question on transformations of graphs. I seem to have a little difficulty in finding the plots for graphs that are 'stretched' or 'shrunk'. For example: f(x)=x^2 is the ba      Log On


   

Question 26621: I have a question on transformations of graphs. I seem to have a little difficulty in finding the plots for graphs that are 'stretched' or 'shrunk'. For example: f(x)=x^2 is the basic quadratic function
g(x)= 2(x-1)^2+3 is the transformed function.
Do I solve g(x) by inserting the results from f(x) in for x into g(x) equation or do I solve g(x) by inserting the original x I used to solve f(x)? Also, is it correct to use BEDMAS and solve inside the brackets, then exponents then multiply?
Thanks a bunch
Answer by longjonsilver(2297) About Me  (Show Source):
You can put this solution on YOUR website!
ok...you need to LEARN --> yes LEARN what each type of transformation does to a basic function. This is the best way forward, as boring as it sounds.

Anyway, that said...here goes:

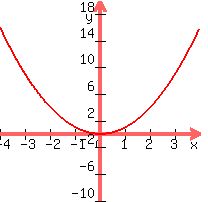
f(x) = x%5E2 is the base function, looking like graph%28200%2C200%2C+-4%2C4%2C+-10%2C20%2C+x%5E2%29

Note from this, that the only solution/root is at x=0.

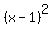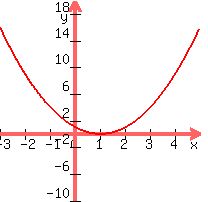Now, f(x) = %28x-1%29%5E2 is the same form of equation, but its 1 root is at x=1... ie the curve has been MOVED to the right by 1 unit: graph%28200%2C200%2C+-3%2C5%2C+-10%2C20%2C+%28x-1%29%5E2%29.

--> The curve crosses the y-axis at y=1 --> needs to be put in!

Now, we will scale all these points by a factor of 2. Note... the point touching the x-axis --> multiply this by 2 and you still get zero. In other words, the curve is still "held" at the same point.

However, the point that it crosses the y-axis is now y=2 --> put it in!

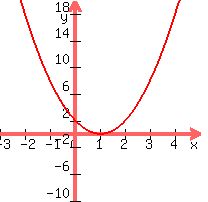graph%28200%2C200%2C+-3%2C5%2C+-10%2C20%2C+2%28x-1%29%5E2%29: I have kept the same axes, so you can see the effect of the scaling.

Finally, we will add 3 to every point. So, no matter what we had, we add 3. This has the effect of moving the whole curve up by 3 units... graph%28200%2C200%2C+-3%2C5%2C+-5%2C25%2C+2%28x-1%29%5E2%2B3%29

So, that is your answer for g(x). Truth be known, I ALWAYS follow this process on paper. Some might be able to do it in their heads, fair play, but for us mortals, do every step on paper. The more you do, the faster you become.

jon.