Question 260766: determine whether the line is PQ is parallel or perpendicular to line with a slope of -2.
P(5,6)
Q (9,8)
Answer by PRMath(133)   (Show Source): (Show Source):
You can put this solution on YOUR website! determine whether the line is PQ is parallel or perpendicular to line with a slope of -2.
P(5,6)
Q (9, 8)
Ok, here are two things you have to know:
If lines are PARALLEL, they have the SAME slope.
If lines are PERPENDICULAR, their slopes are negative reciprocals of one another. In other words, if one slope is 2 the negative reciprocal is 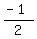 . If one slope is -2, then the negative reciprocal is . If one slope is -2, then the negative reciprocal is  . .
Ok, so you are given that you have a line with a slope of -2. Next you are asked if line PQ is parallel or perpendicular to the line with a slope of -2.
Ok, let's just find the slope for line PQ. The way to find slope is to use this formula:
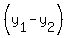 / /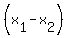
Now let's plug in the info from PQ
P(5,6)
Q (9, 8)
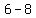 / /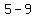 which is which is
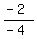 which is which is
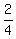 which reduces to which reduces to

The slope of line PQ is: 
The slope we were given was -2. The slope of PQ is  . Therefore, because . Therefore, because  is the negative reciprocal of -2, the two lines are PERPENDICULAR. is the negative reciprocal of -2, the two lines are PERPENDICULAR.
If you get nervous about the use of negative reciprocals, just do one final check. Multiply the first slope times the 2nd. If the answer is -1, then the slopes are indeed negative reciprocals of one another.
So let's do that:
 x x  = =  which is which is 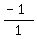 which is -1. which is -1.
Ok, that's your final check. The lines are perpendicular.
I hope this helps you. :-)
|
|
|