Are you writing 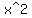 for
for  , etc.?
Did you know that
, etc.?
Did you know that 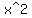 means
means  , not
, not  and there is a big difference between them.
I will assume you meant this:
and there is a big difference between them.
I will assume you meant this:
Determine if the following maximum linear programming problem is in standard form. Do NOT solve.
Maximize 
Subject to the constraints:





It is equivalent to this:
Maximize  subject to the constraints:
subject to the constraints:





 Which is the way the standard form is usually given,
So I would say it is in standard form.
Then you would set it up this way:
Which is the way the standard form is usually given,
So I would say it is in standard form.
Then you would set it up this way:
 then you'd change it to this form:
then you'd change it to this form:
 then to this form:
x1 x2 x3 x4 s1 s2 P
---------------------------------------------------
| 1 0 0 0 | 1 0 | 0 | 4 |
| 0 1 1 1 | 0 1 | 0 | 8 |
|---------------------------------------------|-----
| -2 -3 -8 0 | 0 0 | 1 | 0 |
---------------------------------------------------
Then you'd do row operations by pivoting until there
were no negative numbers on the bottom row, and if you
solved it (even though you were told not to), you'd get:
The maximum value of P would be 72
when x1=4, x2=0, x3=8, x4=0.
Edwin
then to this form:
x1 x2 x3 x4 s1 s2 P
---------------------------------------------------
| 1 0 0 0 | 1 0 | 0 | 4 |
| 0 1 1 1 | 0 1 | 0 | 8 |
|---------------------------------------------|-----
| -2 -3 -8 0 | 0 0 | 1 | 0 |
---------------------------------------------------
Then you'd do row operations by pivoting until there
were no negative numbers on the bottom row, and if you
solved it (even though you were told not to), you'd get:
The maximum value of P would be 72
when x1=4, x2=0, x3=8, x4=0.
Edwin