|
Question 251640: A company makes three products, A, B, and C. There are 500 pounds of raw material available. Each unit of product A requires 2 pounds of raw material, each unit of product B requires 2 pounds, and each unit of product C requires 3 pounds. The assembly line has 1,000 hours of operation available. Each unit of product A requires 4 hours, while each unit of products B and C requires 5 hours. The company realizes a profit of $500 for each unit of product A, $600 for each unit of product B, and $1,000 for each unit of product C. How many units of each of the three products should the company make to maximize profits?
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
You can put this solution on YOUR website! A company makes three products, A, B, and C. There are 500 pounds of raw material available. Each unit of product A requires 2 pounds of raw material, each unit of product B requires 2 pounds, and each unit of product C requires 3 pounds. The assembly line has 1,000 hours of operation available. Each unit of product A requires 4 hours, while each unit of products B and C requires 5 hours. The company realizes a profit of $500 for each unit of product A, $600 for each unit of product B, and $1,000 for each unit of product C. How many units of each of the three products should the company make to maximize profits?
Let x = the number of units of A
Let y = the number of units of B
Let z = the number of units of C
Let's make an inequality for the raw materials only:
 Let's make an inequality for the hours of operation only:
Let's make an inequality for the hours of operation only:
 Let's make an equation for the profit P.
Let's make an equation for the profit P.
 So the problem becomes this:
Maximize
So the problem becomes this:
Maximize
 subject to the constraints:
subject to the constraints:


 and of course
and of course  , ,  and and  we introduce non-negative slack variables
we introduce non-negative slack variables  and
and  to make equations out of the two
inequalities, and rewrite the equation for P getting
0 on the right by subtracting the whol right side from
both sides:
2x + 2y + 3z + s1 = 500
4x + 5y + 5z + s2 = 1000
-500x - 600y - 1000z + P = 0
Now we write it so that all the variables appear in all
the equations with a coefficient. When an equation does
not contain a particular variable, it is placed in that
equation with a 0 coefficient. Also we will put in any
understood coefficients of 1. We will write the equations
so that like letters line up vertically:
2x + 2y + 3z + 1s1 + 0s2 + 0P = 500
4x + 2y + 5z + 0s1 + 1s2 + 0P = 1000
-500x - 600y - 1000z + 0s1 + 0s2 + 1P = 0
Put that in partitioned matrix form
x y z s1 s2 P
----------------------------------------------
| 2 2 3 | 1 0 | 0 | 500 |
| 4 2 5 | 0 1 | 0 | 1000 |
|---------------------------------------------|
|-500 -600 -1000 | 0 0 | 1 | 0 |
----------------------------------------------
The indicators are the numbers on the bottom row.
We want to get rid of all the negative indicators
We start with the most negative one, the -1000.
That's the pivot column. I'll color it red and
the two top numbers in the far right blue:
x y z s1 s2 P
----------------------------------------------
| 2 2 3 | 1 0 | 0 | 500 |
| 4 2 5 | 0 1 | 0 | 1000 |
|---------------------------------------------|
|-500 -600 -1000 | 0 0 | 1 | 0 |
----------------------------------------------
Divide each of those blue numbers by the corresponding red number.
500÷3 = 166 2/3 and 1000÷5=200
166 2/3 is the smallest so the pivot element is 5. We make it 1
by multiplying row 1 by 1/3 and then we use that row to make
all the the other numbers in the red column zero.
x y z s1 s2 P
------------------------------------------------
| 2/3 2/3 1 | 1/3 0 | 0 | 500/3 |
| 2/3 -4/3 0 | -5/3 1 | 0 | 500/3 |
|-----------------------------------------------|
|500/3 200/3 0 |1000/3 0 | 1 | 500000/3 |
------------------------------------------------
Now there are no negative indicators on the bottom
row, so that is the final tableau. If there had been
any negative numbers on the bottom row we would have
had to go through the process again.
next we write the equation form:
2/3x + 2/3y + z + 1/3s1 = 500/3
2/3x - 4/3y - 5/3s1 + 1s2 = 500/3
500/3x + 200/3y + 1000/3s1 + P = 500000/3
Solve the bottom equation for P:
p = 500000/3 - (500/3)x - (200/3)y - (1000/3)s1
So the maximum value of P is when we don't subtract
anything from the 500000/3, which is when
x=0, y=0, and s1=0
Substituting in the first equation:
2/3(0) + 2/3(0) + z + 1/3(0) = 500/3
z = 500/3
Substituting in the second equation:
2/3(0) - 4/3(0) - 5/3(0) + 1s2 = 500/3
s2 = 500/3
So the maximum profit of $500000/3 or $166666.67 is obtained when
no A's or B's are made and 500/3 or to make equations out of the two
inequalities, and rewrite the equation for P getting
0 on the right by subtracting the whol right side from
both sides:
2x + 2y + 3z + s1 = 500
4x + 5y + 5z + s2 = 1000
-500x - 600y - 1000z + P = 0
Now we write it so that all the variables appear in all
the equations with a coefficient. When an equation does
not contain a particular variable, it is placed in that
equation with a 0 coefficient. Also we will put in any
understood coefficients of 1. We will write the equations
so that like letters line up vertically:
2x + 2y + 3z + 1s1 + 0s2 + 0P = 500
4x + 2y + 5z + 0s1 + 1s2 + 0P = 1000
-500x - 600y - 1000z + 0s1 + 0s2 + 1P = 0
Put that in partitioned matrix form
x y z s1 s2 P
----------------------------------------------
| 2 2 3 | 1 0 | 0 | 500 |
| 4 2 5 | 0 1 | 0 | 1000 |
|---------------------------------------------|
|-500 -600 -1000 | 0 0 | 1 | 0 |
----------------------------------------------
The indicators are the numbers on the bottom row.
We want to get rid of all the negative indicators
We start with the most negative one, the -1000.
That's the pivot column. I'll color it red and
the two top numbers in the far right blue:
x y z s1 s2 P
----------------------------------------------
| 2 2 3 | 1 0 | 0 | 500 |
| 4 2 5 | 0 1 | 0 | 1000 |
|---------------------------------------------|
|-500 -600 -1000 | 0 0 | 1 | 0 |
----------------------------------------------
Divide each of those blue numbers by the corresponding red number.
500÷3 = 166 2/3 and 1000÷5=200
166 2/3 is the smallest so the pivot element is 5. We make it 1
by multiplying row 1 by 1/3 and then we use that row to make
all the the other numbers in the red column zero.
x y z s1 s2 P
------------------------------------------------
| 2/3 2/3 1 | 1/3 0 | 0 | 500/3 |
| 2/3 -4/3 0 | -5/3 1 | 0 | 500/3 |
|-----------------------------------------------|
|500/3 200/3 0 |1000/3 0 | 1 | 500000/3 |
------------------------------------------------
Now there are no negative indicators on the bottom
row, so that is the final tableau. If there had been
any negative numbers on the bottom row we would have
had to go through the process again.
next we write the equation form:
2/3x + 2/3y + z + 1/3s1 = 500/3
2/3x - 4/3y - 5/3s1 + 1s2 = 500/3
500/3x + 200/3y + 1000/3s1 + P = 500000/3
Solve the bottom equation for P:
p = 500000/3 - (500/3)x - (200/3)y - (1000/3)s1
So the maximum value of P is when we don't subtract
anything from the 500000/3, which is when
x=0, y=0, and s1=0
Substituting in the first equation:
2/3(0) + 2/3(0) + z + 1/3(0) = 500/3
z = 500/3
Substituting in the second equation:
2/3(0) - 4/3(0) - 5/3(0) + 1s2 = 500/3
s2 = 500/3
So the maximum profit of $500000/3 or $166666.67 is obtained when
no A's or B's are made and 500/3 or 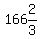 C's are made.
Since you have to make whole products, you can only make 166 C's
and that profit is $166000.
Your teacher probably expects that answer. But if you want to get
precise, you go further:
If you only make 166 C's, then you have used up only 498 pounds of
raw material, and you have 2 pounds of raw materials left over.
That's enough to raw material to make either 1 A or 1 B. We would
choose to make 1 B since the profit is more, $600.
And you've used up only 830 of the 1000 hours of operation,
so you have plenty of operation hours, in fact, 170 left over.
So the exact answer is to make 166 C's and 1 B for a maximum
profit of $166000 + $600 = $166600.
Edwin C's are made.
Since you have to make whole products, you can only make 166 C's
and that profit is $166000.
Your teacher probably expects that answer. But if you want to get
precise, you go further:
If you only make 166 C's, then you have used up only 498 pounds of
raw material, and you have 2 pounds of raw materials left over.
That's enough to raw material to make either 1 A or 1 B. We would
choose to make 1 B since the profit is more, $600.
And you've used up only 830 of the 1000 hours of operation,
so you have plenty of operation hours, in fact, 170 left over.
So the exact answer is to make 166 C's and 1 B for a maximum
profit of $166000 + $600 = $166600.
Edwin
|
|
|
| |