Question 23261: Graphing question?
Graph the following equations.
y=2x-8
3x-2y=-6
Thank you for your help!
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! Please see my lastest TWO Lesson Plans in algebra.com involving the graphing of straight lines. Both Lesson Plans are in the Graphing topic of algebra.com, and because your question here involves TWO different forms of equations, you should see BOTH of the lesson plans--one for each type of problem.
In this problem you have TWO graphs, both of which are straight lines, but they are in different format, and in my opinion, they should be graphed by different methods.
The first graph,  is in SLOPE-INTERCEPT form, which means that you can look at and tell that the y-intercept is the number term, which is -8, and the slope is the coefficient of x, which is 2. Slope is usually written in the form of a fraction: .
In order to draw this graph, start by plotting the y-intercept, which means in this case to go DOWN 8 units on the y-axis and put a point. Now, with your pencil on that point, you need to RISE (that means from the y-intercept point, go UP) 2 units, and RUN (that means go to the RIGHT) 1 unit, and put the next point. Then connect the dots, and it should look like this:
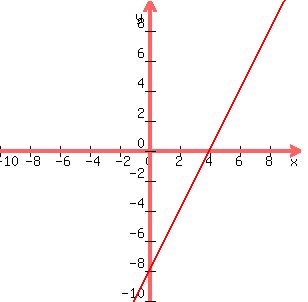
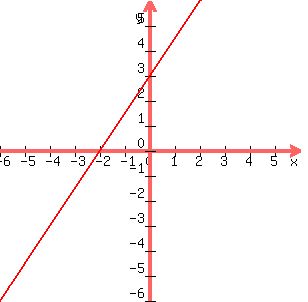
For your second graph, you have an equation in STANDARD FORM. In these cases, it is usually best to find the x and the y intercepts. To find the y-intercept, just let x=0 and find y. To find the x-intercept, just let y=0 and find x.
Let x=0, then -2y =-6, so y = 3
Let y=0, then 3x = -6, so x= -2
Plot those two points, and connect the dots, and it should look like this:
R^2 at SCC
|
|
|
