Question 23221: I need your help! Thank you so much for your assistance!
Graph the system:
y>2x+4
y<-x+8
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! I usually shy away from these inequalites, because I don't know how to shade graphs in algebra.com. However, I can graph the lines and you can do the shading for me.
First graph y = 2x + 4, which is a straight line with y-intercept up 4 units on the y-axis, and a slope of 2.
Because the inequality is ">" you do NOT want to include the line, so graph it with a DOTTED line, and since it is "y> ___" you must shade ABOVE the line.
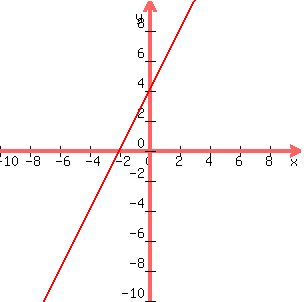
For the next one, graph y = -x + 8, which is a straight line with y-intercept up 8 units on the y-axis, and a slope of -1.
Because the inequality is "<" you do NOT want to include the line, so graph it with a DOTTED line, and since it is "y< ___" you must shade BEWLOW the line.

Now, do it all together on one graph. Remember both lines are to be dotted, and shade above the first line, and below the second line. It should look like this:

In my graph, remember, BOTH lines are DOTTED, and shade ABOVE the red line, and below the green line. The solution is the INTERSECTION of the two areas-- that is the area common to both, the overlapping area, in this case, the upper left part of the graph.
R^2 at SCC
|
|
|