SOLUTION: Suppose the line L has a slope of (-3/5) and passes through the points (11, t) and (2t, -8 ). Find the equation of L and its x and y intercepts.

Algebra ->  Graphs -> SOLUTION: Suppose the line L has a slope of (-3/5) and passes through the points (11, t) and (2t, -8 ). Find the equation of L and its x and y intercepts.      Log On


   

Question 228442: Suppose the line L has a slope of (-3/5) and passes through the points (11, t) and (2t, -8 ). Find the equation of L and its x and y intercepts.
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
Suppose the line L has a slope of (-3/5) and passes through the points (11, t) and (2t, -8 ). Find the equation of L and its x and y intercepts.

Step 1. The slope-intercept form is given as y=mx+b where m is the slope and b is the y-intercept b at x=0 or point (0,b). Here, the slope m=-3/5.

Step 2. The slope m is given as

m=%28y2-y1%29%2F%28x2-x1%29

Step 3. Let (x1,y1)=(11,t) or x1=11 and y1=t and (x2,y2)=(2t,-8) or x2=2t and y2=-8.

Step 4. Now we're given m=-3%2F5. Substituting above values and variables in the slope equation m yields the following steps:

m=%28y2-y1%29%2F%28x2-x1%29

-3%2F5=%28-8-t%29%2F%282t-11%29

Step 5. Multiply 5(2t-11) to both sides to get rid of denominators on both sides of equation.

5%282t-11%29%2A%28-3%2F5%29=5%282t-11%29%28-8-t%29%2F%282t-11%29

-3%282t-11%29=5%28-8-t%29

-6t%2B33=-40-5t

Add 6t+40 to both sides of the equation

-6t%2B33%2B6t%2B40=-40-5t%2B6t%2B40

73=t

Step 6. Therefore the points are (x1,y1)=(11,73) and (x2,y2)=(2*73,-8) or (x2,y2)=(146,-8)

Let's double check the slope m=-3/5 with these two points (11,73) and (146,-8).

m=%28-8-73%29%2F%28146-11%29=-81%2F135=-3%2F5 so it works.

Step 7. Now to get our linear equation, we choose one of the points say (11,73) and the slope m=-3%2F5. We have (x1,y1)=(11,73) or x1=11 and y1=73. Let other point be (x2,y2)=(x,y) or x2=x and y2=y.

Step 8. Now we're given m=-3%2F5. Substituting above values and variables in the slope equation m yields the following steps to get a linear equation:

m=%28y2-y1%29%2F%28x2-x1%29

-3%2F5=%28y-73%29%2F%28x-11%29

Multiply by (x-11) to both sides of the equation

-3%28x-11%29%2F5=y-73

-3x%2F5%2B33%2F5=y-73

Add 73 to both sides of the equation

-3x%2F5%2B33%2F5%2B73=y-73%2B73

-3x%2F5%2B33%2F5%2B365%2F5=y

-3x%2F5%2B398%2F5=y

Step 9. Let's see if the other point (146,-8) satisfies y=-3x%2F5%2B398%2F5 as a check

-8=-3%2A146%2F5%2B398%2F5

-8=-438%2F5%2B398%2F5=-40%2F5

-8=-8 which is a true statement

Step 10. The equation is y=-3x%2F5%2B398%2F5.

Step 11. The x-intercept is when y=0 or

0=-3x%2F5%2B398%2F5 after add 3x/5 and multiplying by 5 to both sides of the equation we have

3x=398

x=398%2F3 ANSWER to finding the x-intercept.

Step 12. The y-intercept is when x=0 or

y=-3%2A0%2F5%2B398%2F5 after add 3x/5 and multiplying by 5 to both sides of the equation we have

y=398%2F5

y=398%2F5 ANSWER to finding the y-intercept.

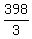Step 13. ANSWER: The equation is y=-3x%2F5%2B398%2F5. The x-intercept is a=398%2F3 or at point (398%2F3, 0). The y-intercept is b=398%2F5 or at point (0,398%2F5).

I hope the above steps were helpful.

For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.

Good luck in your studies!

Respectfully,
Dr J