Question 217410: Write an equation in slope-intercept form that passes through (4, 9) and (5, 12)
Answer by drj(1380)   (Show Source):
You can put this solution on YOUR website! Write an equation in slope-intercept form that passes through (4, 9) and (5, 12)
Step 1. We need to find an equation in slope intercept form given as y=mx+b where m is the slope and b is the y-intercept at point (0,b).
Step 2. The slope of the line m is given as
where for our example is x1=4, y1=9, x2=5 and y2=12 (think of  ). You can choose the points the other way around but be consistent with the x and y coordinates. You will get the same result.
Step 3. Substituting the above values in the slope equation gives
Step 4. The slope is calculated as  or  .
Step 5. Now use the slope equation of step 1 and choose one of the given points. I'll choose point (4,9). Letting y=y2 and x=x2 and substituting m=60 in the slope equation given as,
Step 6. Multiply both sides of equation by (x-4) to get rid of denomination found on the right side of the equation
Step 7. Now simplify and put the above equation into slope-intercept form.
Add 9 to both sides of the equation
ANSWER in slope-intercept form is  where slope m=3 band y-intercept=-3
Step 8. See if the other point (5,12) or x=5 and y=12 satisfies this equation
 So the other point satisfies this equation and lies on the line.
In other words, you can use the other point to check your work.
Note: above equation can be also be transform into standard form as
See graph below to check the above steps. Note the slope and y-intercept as well as the x-intercept.
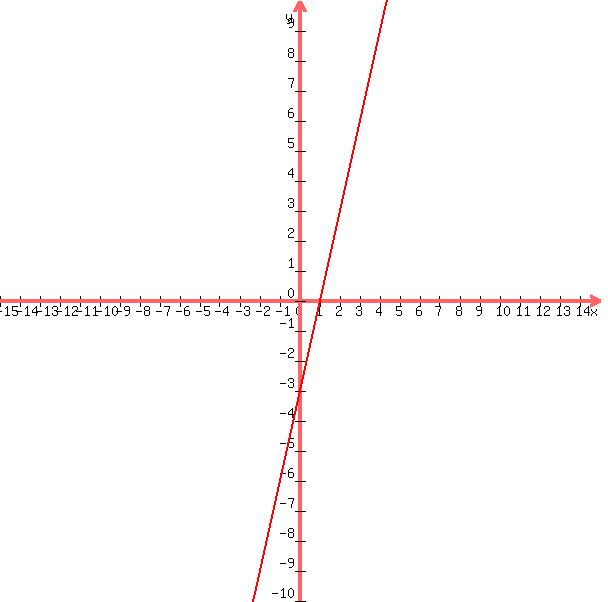
I hope the above steps were helpful.
And good luck in your studies!
For free Step-By-Step Videos on Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra or for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.
Respectfully,
Dr J
|
|
|
