You must clear the first of decimals, and
you must clear the second equation of both
decimals and fractions.
To clear the first equation of decimals we
multiply each term through by 10, and get
We clear the second equation first of fractions
by multiplying each term by 23:
To clear this equation of decimals we
multiply each term through by 10, and get
So the system is now:
We find the least common multiple of the
absolute value of the coefficients of x.
The least common multiple of 3 and 115 is
their product 345.
We divide 3 into 345 and get 115, so we
multiply the first equation by 115:
Now we divide 115 into 345 and get 3, so we
multiply the second equation by -3. We
choose to multiply by a negative number so
they will cancel as you will see
Now we have this system:
We can add the two equations vertically, term
by term, and the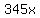 
in the first equation
cancels with the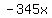 
term in the second.
Upon adding corresponding terms:
or just
So we divide both sides by 
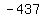
That fraction reduces by dividing top and
bottom by 19:
Now we must find x. In many equations we
would subsatitute the value of x into
one of the equations. However since the
value for y is such an ugly fraction, we
start back with this system:
This time we find the least common multiple of the
absolute value of the coefficients of y.
The least common multiple of 2 and 69 is
their product 138.
We divide 2 into 138 and get 69, so we
multiply the first equation by 69:
Now we divide 69 into 138 and get 2, so we
multiply the second equation by 2. We don't
need to multiply by a negative number this time
because the y terms are already opposit5 in
sing and so they will cancel.
Now we have this system:
We can add the two equations vertically, term
by term, and the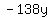 
in the first equation
cancels with the 
term in the second.
Upon adding corresponding terms:
or just
So we divide both sides by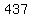 
That fraction reduces by dividing top and
bottom by 19
So the solution is
,
Edwin
