Question 211199: Ok, hello how are you doing today? I am not sure what this question qualifies as under your drop down bar, but I am in college algebra and very stuck on this question. The quesion is about tangent lines and the problem is beneath this statement.
Write the equation of lines that are tangent to the circle x^2+y^2-6x+2y-16=0 when x=2.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ok, hello how are you doing today? I am not sure what this question qualifies as under your drop down bar, but I am in college algebra and very stuck on this question. The quesion is about tangent lines and the problem is beneath this statement.
Write the equation of lines that are tangent to the circle  when when  . .
We find out what points those are by substituting  for for  in in





 and and 
 and and  So the two points of tangency on the circle are
(2,-6) and (2,4).
We plot those points:
So the two points of tangency on the circle are
(2,-6) and (2,4).
We plot those points:
 We know the circle goes through those two points
and we will draw tangents there:
Next we must find the center of the circle, That is
we must get
We know the circle goes through those two points
and we will draw tangents there:
Next we must find the center of the circle, That is
we must get
 in the form
in the form
 We rearrange the terms in the left side,
and get the only constant term on the right
We rearrange the terms in the left side,
and get the only constant term on the right
 Now we want to add two numbers to both sides
in order to complete the squares:
Now we want to add two numbers to both sides
in order to complete the squares:
 Multiplying the coefficient of x, which is
Multiplying the coefficient of x, which is  by by  we get
we get  , then squaring that gives , then squaring that gives  . So we put a . So we put a
 where the red question marks are.
Multiplying the coefficient of y, which is where the red question marks are.
Multiplying the coefficient of y, which is  by by  we get
we get  , then squaring that gives , then squaring that gives  . So we put a . So we put a
 where the green question marks are. where the green question marks are.
 Factor the first three terms on the left, then factor the
last three terms on the left, and combine the terms on the right
Factor the first three terms on the left, then factor the
last three terms on the left, and combine the terms on the right
 So its center is (3,-1) and its radius
is
So its center is (3,-1) and its radius
is  or about or about 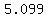 Now we draw the graph of that circle with that center
and radius and draw in the two radii:
Now we draw the graph of that circle with that center
and radius and draw in the two radii:
 Next we want to find the equations of the two tangent lines
drawn below in light green:
Next we want to find the equations of the two tangent lines
drawn below in light green:
 The green tangent lines are perpendicular to the
two radii of the circle drawn above. You want
the equations of them. So to finish, you find the
slopes of the radii, one will be 5 and the other -5,
So you'll use their opposite signed reciprocals,
which will be
The green tangent lines are perpendicular to the
two radii of the circle drawn above. You want
the equations of them. So to finish, you find the
slopes of the radii, one will be 5 and the other -5,
So you'll use their opposite signed reciprocals,
which will be  and and 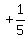 . And then
you'll use the point-slope form to find the equations:
They are: . And then
you'll use the point-slope form to find the equations:
They are:
 and and If you can't do that, post again asking how.
Edwin
If you can't do that, post again asking how.
Edwin
|
|
|