SOLUTION: Hi, Just wondering if anyone can help with the following question, im struggling a bit. For the given vectors find: (a) scalar product and b) angle between the vectors. a = 2

Italicized letters such as a represent vectors
Regular letters represent scalars which are
just plain old numbers.

The scalar product:

That's the kind of multiplying where you multiply
two vectors and get a "non-vector", called a scalar,
which is nothing but a PLAIN OLD NUMBER.

There are two separate formulas for the scalar product.
You use whichever one you need depending on what you
have given.

The first formula is the basic one:

a = mi + nj + pk 
b = qi + rj + sk

a·b = (mi + nj + pk)·(qi + rj + sk) = mq + nr + ps

so for

(2i - j + 3k)·(-i - 7j)

First we rewrite it to show the coefficients
-1 on j in the first and i in the second, and 
put "+ 0k" as a placeholder for the k-component 
in the second one:

(2i - 1j + 3k)·(-1i - 7j + 0k)

m=2, n=-1, p=3, q=-1, r=-7, s=0

So

(mi + nj + pk)·(qi + rj + sk) = mq + nr + ps

becomes

[(2)i + (-1)j + (3)k]·[(-1)i + (-7)j + (0)i] =

(2)(-1) + (-1)(-7) + (3)(0) = -2 + 7 + 0 = 5.

So their scalar product (also called "dot product")
is simply the scalar, (or plain old number), 5.
 
Now we look at the other formula for the scalar product:

a·b = |a||b|cosq where q is the angle between the 

vectors a and b, and where |a| and |b| represent the
scalar (plain old number) magnitude, which is just
the length of the vector. It is found by the extended
Pythagorean formula:

|a| = |mi + nj + pk| = 

Ö(m2 + n2 + p2) 
|b| =

|qi + rj + sk| =
 ____________ 
Ö(q2 + r2 + s2)

So:

|a| = |2i - 1j + 3k| = 
 ___________________
Ö(2)2 + (-1)2 + (3)2 =
 _________
Ö4 + 1 + 9 = 
 __
Ö14

and
 
|b| = |-1i - 7j + 0k| =
 ___________________
Ö(-1)2 + (-7)2 + (0)2 =
 ____________
Ö1 + (49) + 0 = 
 __                                 
Ö50 =
  _______
Ö(25)(2) = 
  _
5Ö2

Substituting in 

a·b = |a||b|cosq
      __                                 _
5 = (Ö14)(5Ö2)cosq
      __
5 = 5Ö28)cosq
      ______
5 = 5Ö(4)(7)*cosq
         _
5 = 5(2)Ö7*cosq
       _                
5 = 10Ö7*cosq
        
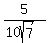 = cosq


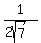 = cosq

Get the inverse cosine of 

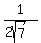q = 79.10° approximately

Edwin