SOLUTION: this is one question with different parts Find the vertex, line of symmetry, maximum or minimum value of the quadratic function, and graph the function. f(x)=-2x^2+2x+3 x-coord

Algebra ->  Graphs -> SOLUTION: this is one question with different parts Find the vertex, line of symmetry, maximum or minimum value of the quadratic function, and graph the function. f(x)=-2x^2+2x+3 x-coord      Log On


   

Question 176168: this is one question with different parts
Find the vertex, line of symmetry, maximum or minimum value of the quadratic function, and graph the function.
f(x)=-2x^2+2x+3
x-coordinate of vertex
y-coordinate of vertex
equation of line of symmetry
max/min value of f(x)
The value of f(1/2)=7/2 is min or max
Please help I have no idea what I am doing thank you
Found 2 solutions by solver91311, MathLover1:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
If you have a function f%28x%29+=+ax%5E2+%2B+bx+%2B+c, you have a parabola with vertex at the point

So, calculate -b%2F2a to get the x-coordinate of the vertex. Then substitute that x-coordinate value into the function and calculate the y-coordinate of the vertex.

The axis of symmetry is the vertical line x+=+v where v is equal to the x-coordinate of the vertex, or v+=+-b%2F2a.

If the lead coefficient, in other words the coefficient on the x%5E2 term is positive, then the parabola is concave up and the vertex is a minimum. If the lead coefficient is negative, then the parabola is concave down and the vertex is a maximum.

To graph the function, first plot the vertex point. Then add a convenient value to the x-coordinate and recalculate the value of the function to get another point on the graph. Because of symmetry, you will also have the same value of the function when you subtract the same amount from the x-coordinate. Perform this process 3 or 4 times to get a set of points and then draw a smooth curve through the plotted points.

Your graph should look like this:

graph%28600%2C600%2C-10%2C10%2C-10%2C10%2C-2x%5E2%2B2x%2B3%29

Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
1. Quadratic into Vertex Form
Solved by pluggable solver: Completing the Square to Get a Quadratic into Vertex Form


y=-2+x%5E2%2B2+x%2B3 Start with the given equation



y-3=-2+x%5E2%2B2+x Subtract 3 from both sides



y-3=-2%28x%5E2-1x%29 Factor out the leading coefficient -2



Take half of the x coefficient -1 to get -1%2F2 (ie %281%2F2%29%28-1%29=-1%2F2).


Now square -1%2F2 to get 1%2F4 (ie %28-1%2F2%29%5E2=%28-1%2F2%29%28-1%2F2%29=1%2F4)





y-3=-2%28x%5E2-1x%2B1%2F4-1%2F4%29 Now add and subtract this value inside the parenthesis. Doing both the addition and subtraction of 1%2F4 does not change the equation




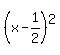
y-3=-2%28%28x-1%2F2%29%5E2-1%2F4%29 Now factor x%5E2-1x%2B1%2F4 to get %28x-1%2F2%29%5E2



y-3=-2%28x-1%2F2%29%5E2%2B2%281%2F4%29 Distribute



y-3=-2%28x-1%2F2%29%5E2%2B1%2F2 Multiply



y=-2%28x-1%2F2%29%5E2%2B1%2F2%2B3 Now add 3 to both sides to isolate y



y=-2%28x-1%2F2%29%5E2%2B7%2F2 Combine like terms




Now the quadratic is in vertex form y=a%28x-h%29%5E2%2Bk where a=-2, h=1%2F2, and k=7%2F2. Remember (h,k) is the vertex and "a" is the stretch/compression factor.




Check:


Notice if we graph the original equation y=-2x%5E2%2B2x%2B3 we get:


graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C-2x%5E2%2B2x%2B3%29 Graph of y=-2x%5E2%2B2x%2B3. Notice how the vertex is (1%2F2,7%2F2).



Notice if we graph the final equation y=-2%28x-1%2F2%29%5E2%2B7%2F2 we get:


graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C-2%28x-1%2F2%29%5E2%2B7%2F2%29 Graph of y=-2%28x-1%2F2%29%5E2%2B7%2F2. Notice how the vertex is also (1%2F2,7%2F2).



So if these two equations were graphed on the same coordinate plane, one would overlap another perfectly. So this visually verifies our answer.






Solved by pluggable solver: Min/Max of a Quadratic Function
The min/max of a quadratic equation is always at a point where its first differential is zero. This means that in our case, the value of x at which the given equation has a maxima/minima must satisfy the following equation:2%2A-2%2Ax%2B2=0
=> x+=+-2%2F%282%2A-2%29+=+0.5

This point is a minima if value of coefficient of x2 is positive and vice versa. For our function the point x=0.5 is a 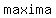maxima The graph of the equation is :
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+-2%2Ax%5E2%2B2%2Ax%2B3+%29
Alternate method


In this method, we will use the perfect square method.


Step one:
Make the coefficient of x%5E2 positive by multiplying it by -1 in casea%3C0.
Maxima / Minima is decided from the sign of 'a'.
If 'a' is positive then we have Minima and for 'a'negative we have Maxima.

Step two:
Now make the perfect square with the same x%5E2 and x coefficient.
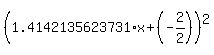
%281.4142135623731%2Ax+%2B+%28-2%2F2%29%29%5E2

Maxima / Minima lies at the point where this squared term is equal to zero.

Hence,
=>x=%28-%28-2%2F2%29%2F1.4142135623731%29=+0.707106781186547

This point is a minima if value of coefficient of x2 is positive and vice versa. For our function the point x=0.5 is a 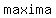maxima.

For more on this topic, refer to Min/Max of a Quadratic equation.