Question 174272:
Omg, hopefully this is the last one. I do not understand this. Please somebody explain it to me and show me how to do these types of word problems. I greatly appreciate it in advance.
Say there's a credit remaining on a phone card (in dollars) is a linear function of the total calling time (in minutes). When graphed, the function gives a line with a slope of -0.12 . :(
There is a $23.00 credit remaining on the card after 25 minutes of calling. How much credit will there be after 33 minutes of calls?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x=number of minutes and y=amount of credit remaining
In order to answer this question, we need to find the equation that models (ie represents) this problem.
Because "There is a $23.00 credit remaining on the card after 25 minutes of calling", this tells us that  and and  which gives the point (25,23). So the line goes through this point. which gives the point (25,23). So the line goes through this point.
Also, since the "function gives a line with a slope of -0.12", this tells us that our line has a slope of -0.12. So this means that 
Note: "a slope of -0.12" tells us that for every minute that we talk, we lose $0.12 (or 12 cents).
If you want to find the equation of line with a given a slope of 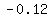 which goes through the point (25,23), simply use the point-slope formula to find the equation: which goes through the point (25,23), simply use the point-slope formula to find the equation:
---Point-Slope Formula---
 where where  is the slope, and is the slope, and ) is the given point is the given point
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Distribute Distribute 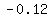
 Multiply Multiply 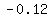 and and  to get to get 
 Add 23 to both sides to isolate y Add 23 to both sides to isolate y
 Combine like terms Combine like terms
So the equation of the line with a slope of 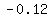 which goes through the point (25,23) is which goes through the point (25,23) is 
So this means that the equation tying together the amount remaining "y" and the number of minutes "x" is 
How much credit will there be after 33 minutes of calls?
To answer this question, we'll use the equation we just found.
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply
 Add Add
So after 33 minutes of calls, there will be $22.04 of credit left.
|
|
|