SOLUTION: I don't understand how to do this problem? 3x+y=5 -2x+3y=4

Algebra ->  Graphs -> SOLUTION: I don't understand how to do this problem? 3x+y=5 -2x+3y=4      Log On


   

Question 168961: I don't understand how to do this problem?
3x+y=5
-2x+3y=4
Found 3 solutions by josmiceli, stanbon, Electrified_Levi:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
(1) 3x+%2B+y+=+5
(2) -2x+%2B+3y+=+4
This is 2 equations with 2 unknowns, so it's solvable
Multiply (1) by 3 and subtract (2) from (1)
To subtract, change all the signs of (2) to minus
9x+%2B+3y+=+15
-%28-2x%29+-+3y+=+-4
Now I'll rewrite these
9x+%2B+3y+=+15
2x+-+3y+=+-4
The result is:
11x++=+11
x+=+1
Substitute this result back in (1)
(1) 3x+%2B+y+=+5
(1) 3%2A1+%2B+y+=+5
y+=+5+-+3
y+=+2
The solutions are x = 1 and y = 2

Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
3x+y=5
-2x+3y=4
--------------
Multiply thru the 1st equation by 3:
9x+3y = 15
-2x+3y = 4
---------------
Subtract the 2nd from the 1st to get:
11x = 11
X = 1
-----------
Substitute this into 3x+y=5 to solve for "y":
3*1 + y = 5
y = 2
---------------
Ans: (1,2)
================
Cheers,
Stan H.

Answer by Electrified_Levi(103) About Me  (Show Source):
You can put this solution on YOUR website!
Hi, Hope I can help,
.
3x+y=5
-2x+3y=4
.
There are several ways to solving these systems of equations, I will show you an overall easy way of doing it
.
First, solve for a letter, usually the easiest one, we will solve for "y" in both equations
.
First equation, +3x%2By=5+, we need to move "3x" to the right side
.
+3x%2By=5+ = +3x-3x%2By=5-3x+ = +y=5-3x+ or +y+=+%28-3x%29+%2B+5+, if we rearrange it.
.
Our first answer is 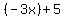+%28-3x%29+%2B+5+
.
Let us solve for "y" in the second equation, +-2x%2B3y=4+
.
+-2x%2B3y=4+, first we need to move (-2x) to the right side
.
+-2x%2B3y=4+ = +-2x%2B2x%2B3y=4%2B2x+ = +3y=4%2B2x+ or +3y=2x%2B4+, rearranging it
.
+3y=2x%2B4+, now we need to divide each side by "3" to get "y"
.
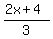+3y=2x%2B4+ = +3y%2F3=%282x%2B4%29%2F3+ = +y=%282x%2B4%29%2F3+
.
+%282x%2B4%29%2F3+ is our second answer
.
Since "y" equals one number both of our answers will equal each other
.
First answer = 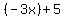+%28-3x%29+%2B+5+
.
Second answer = 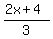+%282x%2B4%29%2F3+
.
These two answers will equal each other
.
+%28-3x%29+%2B+5+=+%282x%2B4%29%2F3+ = +%28%28-3x%29+%2B+5%29%2F1+=+%282x%2B4%29%2F3+, we will use cross- multiplication
.
+highlight%28%28-3x%29+%2B+5%29%2F1+=+%282x%2B4%29%2Fhighlight%283%29+ = +%28%28-3x%29+%2B+5%29%2Fhighlight%281%29+=+highlight%282x%2B4%29%2F3+
.
+%28%28-3x%29+%2B+5%29%283%29+=+%281%29%282x%2B4%29+, rearranging the left side
.
+%283%29%28%28-3x%29+%2B+5%29+=+%281%29%282x%2B4%29+, now we can use the distribution method
.
=
.
Remember the negative and positive signs
.
+-9x+%2B+15+=+2x+%2B+4+
.
Now we can solve for "x", let us move (-9x) to the right side
.
+-9x+%2B+15+=+2x+%2B+4+ = +-9x+%2B+9x+%2B+15+=+2x+%2B+9x+%2B+4+ = +15+=+11x+%2B+4+, now we need to move "4" to the left side
.
+15+=+11x+%2B+4+ = +15+-+4+=+11x+%2B+4+-+4+ = +11+=+11x+, now we can divide each side to find "x"
.
+11+=+11x+ = +11%2F11+=+11x%2F11+ = +1+=+x+, +x+=+1+, you can check by replacing "x" with "1" in the equation +%28-3x%29+%2B+5+=+%282x%2B4%29%2F3+
.
+%28-3x%29+%2B+5+=+%282x%2B4%29%2F3+ = +%28-3%281%29%29+%2B+5+=+%282%281%29%2B4%29%2F3+ = +%28-3%29+%2B+5+=+%282%2B4%29%2F3+ = +2+=+%286%29%2F3+ = +2+=+2+ ( True )
.
+x+=+1+, to find "y", replace "x" with "1" in one of the two original equations
.
3x+y=5
-2x+3y=4
.
We will use the first equation
.
+3x%2By=5+ = +3%281%29%2By=5+ = +3%2By=5+, now we will move "3" to the right side
.
+3+-+3+%2By=5+-+3+ = +y=+2+
.
+x+=+1+
.
+y+=+2+
.
We can check our answers by replacing both "x" and "y" in the two original equations. ( x = 1 ) ( y = 2 )
.
+3x%2By=5+ = +3%281%29%2B%282%29=5+ = +3%2B2=5+ = +5+=+5+ ( True )
.
+-2x%2B3y=4+ = +-2%281%29%2B3%282%29=4+ = +-2%2B6=4+ = +4+=+4+ ( True )
.
+x+=+1+
.
+y+=+2+
.
A solution set is in the form (x,y), our solution set is ( 1, 2 )
.
Hope I helped, Levi