SOLUTION: sketch the graph of the function. label the vertex. y=x<sup>2</sup>-x-5

Algebra ->  Graphs -> SOLUTION: sketch the graph of the function. label the vertex. y=x<sup>2</sup>-x-5      Log On


   

Question 152607: sketch the graph of the function. label the vertex.
y=x2-x-5
Found 2 solutions by jim_thompson5910, mducky2:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

Table of Contents:


Jump to Table
Jump to Graph


In order to graph y=x%5E2-x-5, we need to plot some points.


Let's find y when x=-2
(Note: you can start with any x-value):


y=x%5E2-x-5 Start with the given equation.


y=%28-2%29%5E2--2-5 Plug in x=-2.


y=%28-2%29%5E2%2B2-5 Simplify.


y=1%284%29%2B2-5 Square -2 to get 4.


y=4%2B2-5 Multiply 1 and 4 to get 4.


y=1 Combine like terms.


So when x=-2, then y=1.


So we have the point .


----------------------------------------------------


Let's find y when x=-1:


y=x%5E2-x-5 Start with the given equation.


y=%28-1%29%5E2--1-5 Plug in x=-1.


y=%28-1%29%5E2%2B1-5 Simplify.


y=1%281%29%2B1-5 Square -1 to get 1.


y=1%2B1-5 Multiply 1 and 1 to get 1.


y=-3 Combine like terms.


So when x=-1, then y=-3.


So we have the point .


----------------------------------------------------


Let's find y when x=0:


y=x%5E2-x-5 Start with the given equation.


y=%280%29%5E2-0-5 Plug in x=0.


y=1%280%29-0-5 Square 0 to get 0.


y=0-0-5 Multiply 1 and 0 to get 0.


y=-5 Combine like terms.


So when x=0, then y=-5.


So we have the point .


----------------------------------------------------


Let's find y when x=1:


y=x%5E2-x-5 Start with the given equation.


y=%281%29%5E2-1-5 Plug in x=1.


y=1%281%29-1-5 Square 1 to get 1.


y=1-1-5 Multiply 1 and 1 to get 1.


y=-5 Combine like terms.


So when x=1, then y=-5.


So we have the point .


----------------------------------------------------


Let's find y when x=2:


y=x%5E2-x-5 Start with the given equation.


y=%282%29%5E2-2-5 Plug in x=2.


y=1%284%29-2-5 Square 2 to get 4.


y=4-2-5 Multiply 1 and 4 to get 4.


y=-3 Combine like terms.


So when x=2, then y=-3.


So we have the point .


----------------------------------------------------


Let's find y when x=3:


y=x%5E2-x-5 Start with the given equation.


y=%283%29%5E2-3-5 Plug in x=3.


y=1%289%29-3-5 Square 3 to get 9.


y=9-3-5 Multiply 1 and 9 to get 9.


y=1 Combine like terms.


So when x=3, then y=1.


So we have the point .


----------------------------------------------------





Jump to Top of Page
Now let's make a table of the values we just found.


Table of Values:





xy
-21


-1-3


0-5


1-5


2-3


31

Now let's plot the points:







Jump to Top of Page

Graph:


Now draw a curve through all of the points to graph y=x%5E2-x-5:


Graph of y=x%5E2-x-5

Answer by mducky2(62) About Me  (Show Source):
You can put this solution on YOUR website!
In order to sketch the graph of a function, we need to know the basic shape. We know that anything with x2 will be parabola which opens upwards and has its vertex on its bottom. It should have the same basic shape as this graph:

+graph%28+300%2C+200%2C+-5%2C+5%2C+-5%2C+5%2C+x%5E2%29+


Now we need to find some points on the graph. Since the problem asks for it, a good place to start would be the vertex. In any equation ax2 + bx + c, the points of the vertex (h,k) can be found using this equation:
h+=+-b%2F2a

Let's plug in the numbers from our equation, x2 - x - 5
h+=+-%28-1%29%2F2%281%29
h+=+1%2F2

Now we can find k by plugging it back into our function:
k+=+x%5E2+-+x+-+5
k+=+%281%2F2%29%5E2+-+%281%2F2%29-5
k+=+%281%2F4%29+-+%281%2F2%29+-+5
k+=+-21%2F4

Therefore, the vertex is (1/2,-21/4).

Let's find a point on the y-axis this time. The point on the y-axis will have an x = 0:
y+=+x%5E2+-+x+-+5
y+=+0%5E2+-+0+-+5
y+=+0+-+0+-+5
y+=+-5

Now we have a new point: (0,-5)

Since we know that quadratic equations are parallel, we know there has to be another point with the same y value, opposite the same distance from the axis of symmetry of the parabola.
Distance from axis of symmetry: abs%280-%281%2F2%29%29+=+1%2F2

Since 0 < 1/2, the other point on the y-axis must be to the left of the axis of symmetry, so lets add twice the distance:
Twice the distance: 0+%2B+2%281%2F2%29+=+1

Now we have a new point at (1,-5)

Just to make it easier to graph, let's find some other points on the graph with numbers that are easy to plug into the equation.

If x = 2:
y+=+2%5E2+-+2+-+5
y+=+4+-+7
y+=+-3

As with the y-intercept, we know that there has to be a symmetrical point on the other side of the line of symmetry. Using the same technique:
Distance from axis of symmetry: abs%282-%281%2F2%29%29+=+3%2F2

Since 2 > 1/2, the other point must be on the left side of the equation, meaning we need to subtract twice the distance:
Twice the distance: 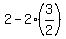2+-+2%283%2F2%29
= 2+-+3
= -1

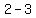
Now we have two more points: (2,-3) and (-1,-3)


Let's plot the points we have:

(-1/2,-21/4)
(0,-5)
(1,-5)
(2,-3)
(-1,-3)


+graph%28+300%2C+200%2C+-5%2C+5%2C+-6%2C+6%2C+x%5E2-x-5%29+

Be sure to label the vertex at (-1/2, -21/4).