SOLUTION: Use the rational roots theorem to solve: p(x)=x^4-5x^3+5x^2+5x-6

Use the rational roots theorem to solve:


The last term is -6, which in absolute value is 6, and which
has these factors 1,2,3,6

The leading term (the term with largest exponent) is , has
coefficient 1, which in absolute value is 1, and which
has only the one factor 1.

Now we form all the fractions with numerator 1,2,3,or 6 and
denominator 1

These are , , 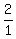,  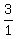or

          , , , .

Their negatives are also possible rational roots, so all the
possible rational roots are:

          ±, ±, ±, ± 

We start out by trying  using synthetic division to
see if we get a 0 remainder:

      1| 1 -5  5  5 -6
       |    1 -4  1  6
         1 -4  1  6  0

Yes we do get 0 remainder, so we know that we have factored
the polynomial

  

   as



So now we can just find the roots of the simpler polynomial:

     

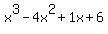The first and last numbers happen to be the same as they were
in the original, so we can try the same ones again.  We try 1
again:

      1| 1 -4  1  6
       |    1 -3 -2
         1 -3 -2  4  

No that leaves a remainder of 4, not 0.

So we try -1

     -1| 1 -4  1  6
       |   -1  6 -6
         1 -5  6  0

Yes we do get 0 remainder, so we know that we have factored
the polynomial again.

First we factored

  

   as

  

Now we have factored the polynomial in the 
second parentheses, and we have:



So now we can just find the roots of the simpler polynomial:

     

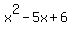But we don't need to do synthetic division again, for
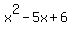 factors as 

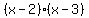So now we have factored  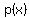completely:



Set each factor equal to 0 and so the roots are 

, , , 

Edwin