Question 146970: f(x) = x ^2 + 10x -19. Identify the vertex and intercept(s).
Thank You
Found 2 solutions by nabla, stanbon:
Answer by nabla(475)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider this form:
ax^2+bx+c=f(x).
We can derive the formula for the vertex using calculus.
df/dx=2ax+b
This gives the slope of the function at any x. Now, when the slope is zero, there is a maximum or minimum for quadratic equations. This will also be the vertex.
So,
0=2ax+b
x=-b/2a is the x-coordinate of the vertex.
So for our problem here,
x=-10/2=-5.
Which gives f(-5)=25-50-19=-44
So (-5,-44) is the vertex.
Now, the y-intercept is where x is zero, namely f(0).
So, f(0)=-19. This is the y-intercept. (0,-19).
Moreover, the x-intercepts are where y is zero, namely f(x)=0.
So, 0=x^2+10x-19. For this we shall use the quadratic formula

| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=176 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 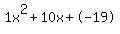 can be factored: can be factored:

Again, the answer is: 1.6332495807108, -11.6332495807108.
Here's your graph:
 |
Finally, a graph:

Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x) = x ^2 + 10x -19. Identify the vertex and intercept(s).
-----------
The vertex occurs when x= -b/2a = -10/(2*1)= -5
f(-5) = (-5)^2 + 10*-5 -19 = 25-50-19 = -44
So, vertex is at (-5,-44)
--------------
x-intercept
Let f(x) = 0 and solve for "x":
x^2+10x-19 = 0
x = [-10 +- sqrt(100-4*-19)]/2
x = [-10 +- sqrt(176)]/2
x = [-10 +- 4sqrt(11)]/2
x = [-5 +- 2sqrt(11)]
x-intercept at (-5+2sqrt(11),0) and at (-5-2sqrt(11),0)
---------------
y-intercept
Let x = 0, then f(0) = -19
y-intercept at (0.-19)
==================
Graph:

Cheers,
Stan H.
|
|
|