
 First I'll approach it graphically to see what
to expect; then I'll do it algebraically
The graph of
First I'll approach it graphically to see what
to expect; then I'll do it algebraically
The graph of  is this parabola:
is this parabola:
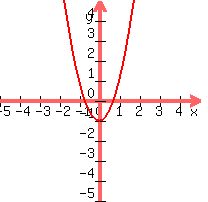 The graph of
The graph of  is this ellipse:
is this ellipse:
 Put them together on one graph:
The graph of
Put them together on one graph:
The graph of  is this ellipse:
is this ellipse:
 Since these graphs cross in two points, these will be two
real solutions, and since parabolas and circles could cross
as many as 4 times, there will two imaginary solutions as well
Since these graphs cross in two points, these will be two
real solutions, and since parabolas and circles could cross
as many as 4 times, there will two imaginary solutions as well

 The first equation is already solved for
The first equation is already solved for  , so we substitute
, so we substitute
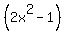 for
for  in the second equation:
in the second equation:







 That does not factor, so we solve that for
That does not factor, so we solve that for  using the quadratic formula:
using the quadratic formula:
 where
where  ,
,  ,
, 


 So we have two solutions for
So we have two solutions for 
 and
and  If we substitute the first value of
If we substitute the first value of  in
in  , we get
, we get
 If we substitute the second value of
If we substitute the second value of  in
in  , we get
, we get
 The first value of
The first value of  gives these two solutions for x:
gives these two solutions for x:
 and
and  The second value of
The second value of  gives these two solutions for x:
gives these two solutions for x:
 ,
,  ,
but since
,
but since 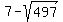 is a negative number, it's going to be
imaginary, so we factor
is a negative number, it's going to be
imaginary, so we factor  out of it,
out of it, 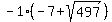 ,
so we have
,
so we have
 and of course
and of course  So we have four solutions for (
So we have four solutions for ( ,
, )
(
)
( ,
, 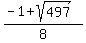 ) = (
) = ( ,
, 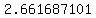 )
(
)
(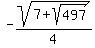 ,
, 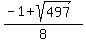 ) = (
) = (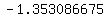 ,
, 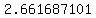 )
These are the points where the curves above cross, and are the two
real solutions.
Here are the two imaginary solutions:
(
)
These are the points where the curves above cross, and are the two
real solutions.
Here are the two imaginary solutions:
(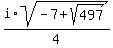 ,
, 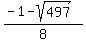 )
(
)
( ,
, 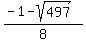 )
Edwin
)
Edwin