Question 143722: 1. Solve  by completing the square. Find exact solutions. by completing the square. Find exact solutions.
Then:
a. Find the vertex.
b. Find the line of symmetry.
c. Determine whether there is a maximum or minimum value and find that value.
d. Show a sketch of the graph.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Start with the given equation Start with the given equation
Take half of the x-coefficient 8 to get 4 (ie  ) )
Now square 4 to get 16. (ie  ) )
 Add this result to both sides Add this result to both sides
 Combine like terms Combine like terms
 Factor Factor  to get to get 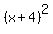 . (note: if you need help with factoring, check out this solver) . (note: if you need help with factoring, check out this solver)
 Take the square root of both sides Take the square root of both sides
 Subtract 4 from both sides Subtract 4 from both sides
 Simplify Simplify 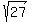 to get to get  . (note: If you need help with simplifying square roots, check out this solver) . (note: If you need help with simplifying square roots, check out this solver)
So the solutions are
 or or 
-----------------------------
a)
 Start with the given equation Start with the given equation
 Subtract 11 from both sides Subtract 11 from both sides
To find the vertex, we first need to find the axis of symmetry (ie the x-coordinate of the vertex)
To find the axis of symmetry, use this formula:

From the equation  we can see that a=1 and b=8 we can see that a=1 and b=8
 Plug in b=8 and a=1 Plug in b=8 and a=1
 Multiply 2 and 1 to get 2 Multiply 2 and 1 to get 2
 Reduce Reduce
So the axis of symmetry is 
So the x-coordinate of the vertex is  . Lets plug this into the equation to find the y-coordinate of the vertex. . Lets plug this into the equation to find the y-coordinate of the vertex.
Lets evaluate 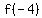
 Start with the given polynomial Start with the given polynomial
 Plug in Plug in 
 Raise -4 to the second power to get 16 Raise -4 to the second power to get 16
 Multiply 8 by -4 to get -32 Multiply 8 by -4 to get -32
 Now combine like terms Now combine like terms
So the vertex is (-4,-27)
b)
From part a) we found the axis of symmetry to be 
c)
Looking at  , we can see that , we can see that  , ,  , and , and  . Since . Since  , this tells us that the parabola opens upward and that there is a minimum. , this tells us that the parabola opens upward and that there is a minimum.
To find the minimum, we only need to look at the vertex. Since the vertex is the point (-4,-27), this means that the minimum is 
d)
Here's a sketch to visually verify our answers
 Graph of Graph of 
|
|
|