Question 125831: 6. Determine which of the ordered pairs are solutions for the given equation.
(0, -2) (0, -1) (1/2 , 0) (3, -5)
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website!  Start with the given equation
Let's test the first solution (0,-2):
 Plug in  and 
 Simplify. Since the two sides of the equation are not equal, this means (0,-2) is not a solution to
-------Now lets test another solution-------
Let's test the second solution (0,-1):
 Plug in and 
 Simplify. Since the two sides of the equation are equal, this means (0,-1) is a solution to
-------Now lets test another solution-------
Let's test the third solution (1/2,0):
 Plug in  and 
 Multiply
 Reduce
 Subtract. Since the two sides of the equation are equal, this means (1/2,0) is a solution to
-------Now lets test another solution-------
Let's test the fourth solution (3,-5):
 Plug in  and 
 Simplify. Since the two sides of the equation are not equal, this means (3,-5) is not a solution to
==============================================================================
Answer:
So the following ordered pairs are solutions to
(0,-1) and (1/2,0)
Now let's graph the equation and plot the points (0,-2), (0,-1), (1/2,0) and (3,-5)
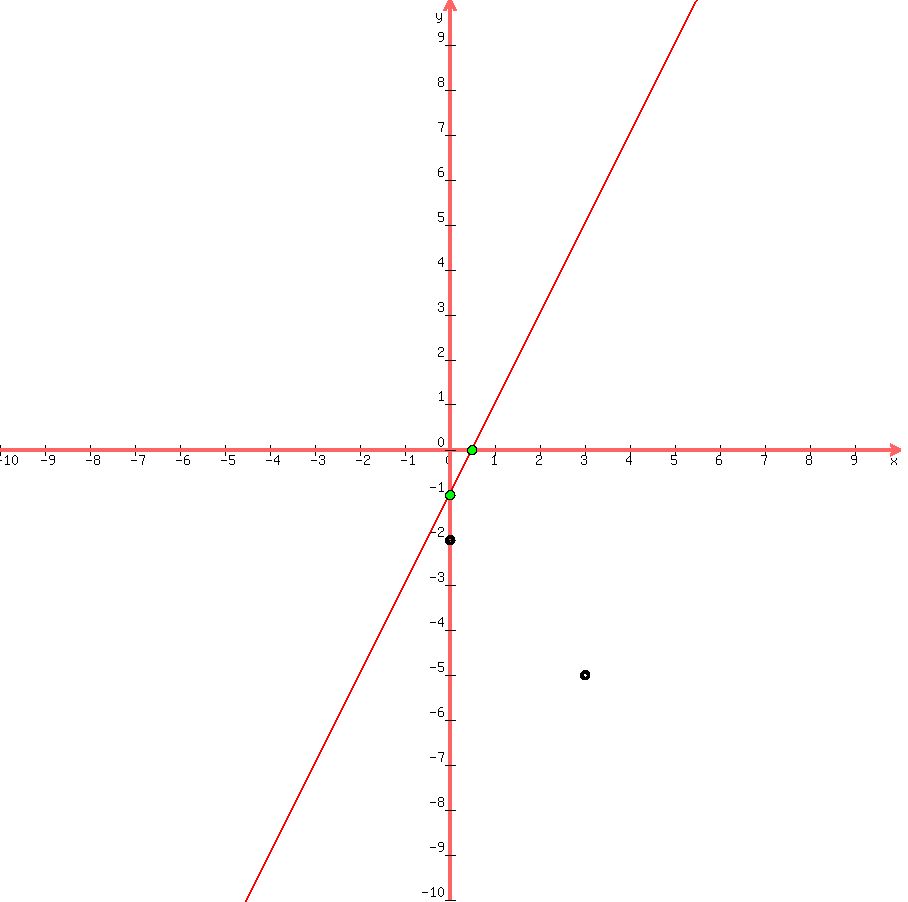
Here we can see that the points (0,-1) and (1/2,0) lie on the line (they are the green points). These are the solutions to the equation .
Notice the other possible solutions are points that do not lie on the line. Those ordered pairs do not satisfy the equation
|
|
|
