SOLUTION: Graph the equations. (1) y = x + 1 (2) y = 2x squared

Algebra ->  Graphs -> SOLUTION: Graph the equations. (1) y = x + 1 (2) y = 2x squared      Log On


   

Question 122814: Graph the equations.
(1) y = x + 1
(2) y = 2x squared
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
# 1



Looking at y=x%2B1 we can see that the equation is in slope-intercept form y=mx%2Bb where the slope is m=1 and the y-intercept is b=1


Since b=1 this tells us that the y-intercept is .Remember the y-intercept is the point where the graph intersects with the y-axis

So we have one point




Now since the slope is comprised of the "rise" over the "run" this means
slope=rise%2Frun

Also, because the slope is 1, this means:

rise%2Frun=1%2F1


which shows us that the rise is 1 and the run is 1. This means that to go from point to point, we can go up 1 and over 1



So starting at , go up 1 unit


and to the right 1 unit to get to the next point



Now draw a line through these points to graph y=x%2B1

So this is the graph of y=x%2B1 through the points and








# 2

In order to graph y=2x%5E2, we need to plot some points.

We can start at any x value, so lets start at x=-2




Lets evaluate 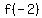f%28-2%29

f%28x%29=2x%5E2 Start with the given polynomial


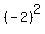f%28-2%29=2%28-2%29%5E2 Plug in x=-2


f%28-2%29=2%284%29 Evaluate %28-2%29%5E2 to get 4

f%28-2%29=%2B8 Multiply 2 and 4 to get 8




So when x=-2, f%28x%29=8 which means our 1st point is (-2,8)



-------Now lets find another point-------



Lets evaluate 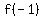f%28-1%29

f%28x%29=2x%5E2 Start with the given polynomial


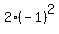f%28-1%29=2%28-1%29%5E2 Plug in x=-1


f%28-1%29=2%281%29 Evaluate 2%28-1%29%5E2 to get 21

f%28-1%29=%2B2 Multiply 2 and 1 to get 2




So when x=-1, f%28x%29=2 which means our 2nd point is (-1,2)



-------Now lets find another point-------



Lets evaluate f%280%29

f%28x%29=2x%5E2 Start with the given polynomial


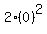f%280%29=2%280%29%5E2 Plug in x=0


f%280%29=2%280%29 Evaluate 2%280%29%5E2 to get 20

f%280%29=0 Multiply 2 and 0 to get 0


So when x=0, f%28x%29=0 which means our 3rd point is (0,0)



-------Now lets find another point-------



Lets evaluate f%281%29

f%28x%29=2x%5E2 Start with the given polynomial


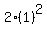f%281%29=2%281%29%5E2 Plug in x=1


f%281%29=2%281%29 Evaluate 2%281%29%5E2 to get 21

f%281%29=%2B2 Multiply 2 and 1 to get 2




So when x=1, f%28x%29=2 which means our 4th point is (1,2)



-------Now lets find another point-------



Lets evaluate f%282%29

f%28x%29=2x%5E2 Start with the given polynomial


f%282%29=2%282%29%5E2 Plug in x=2


f%282%29=2%284%29 Evaluate 2%282%29%5E2 to get 24

f%282%29=%2B8 Multiply 2 and 4 to get 8

f%282%29=%2B8 Multiply 0 and to get 0

f%282%29=8 Now combine like terms


So when x=2, f%28x%29=8 which means our 5th point is (2,8)






Now lets make a table of the values we have calculated 



 xy



 -28
 

 -12
 

 00
 

 12
 

 28
Now plot the points



Now connect the points to graph y=2x%5E2 (note: the more points you plot, the easier it is to draw the graph)