Question 1208022: Assume that f(3) = 4. Name a point that must be on the graph of y= -5f(2x - 3) + 1
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
Assume that f(3) = 4. Name a point that must be on the graph of y= -5f(2x - 3) + 1
~~~~~~~~~~~~~~~~~~~~~~~~
First, we want the argument 2x-3 be 3.
So, we write this equation
2x - 3 = 3.
Then we solve it and find x = 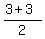 =  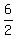= 3.
Next, we want to calculate y = -5f(2x-3) + 1.
We just know that 2x-3 is 3, because we found x in this way.
So, we write
y = = -5f(3) + 1 = (at this point, we know and use that f(3)=4, so we continue) = -5*4 + 1 = -20 + 1 = -19.
Thus the point (x,y) = (3,-19) is on the graph y = -5f(2x-3) + 1.
ANSWER. If f(3) = 4, then the point which must be on the graph y = -5f(2x-3) + 1 is (x,y) = (3,-19).
Solved.
--------------------------
It is a real  for you to solve many other similar problems.
To start, you should say to yourself "First, we want . . . "
These words are magic.
As soon as you pronounce them, all necessary words and thoughts that follow, will flow by themselves.
////////////////////
To see other similar solved problems, look into the lesson
- Given a point on a plot of a function, find the corresponding point on the plot of transformed function
in this site.
It is to make your horizon wider.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
I'll go over a similar example.
Problem
Given f(4) = 5
Find a point on g(x) = 2*f(3x+1) + 7
Solution
Compare f(4) with f(3x+1)
Equate the inputs and solve for x.
4 = 3x+1
3x = 4-1
3x = 3
x = 3/3
x = 1
Therefore x = 1 leads to 3x+1 = 4.
If x = 1 then f(3x+1) = f(4) = 5.
Then,
g(x) = 2*f(3x+1) + 7
g(1) = 2*f(3*1+1) + 7
g(1) = 2*f(4) + 7
g(1) = 2*5 + 7
g(1) = 10 + 7
g(1) = 17
We have shown that (1,17) is on g(x).
Keep in mind this is likely not the final answer to your particular question, but you can use it as a template to solve.
|
|
|
