SOLUTION: i am having trouble solving problems similar to this: Write an equation of the line that passes throuhg the given point and is parallel to the given line. (4,5),y=x+6. I would muc

Algebra ->  Graphs -> SOLUTION: i am having trouble solving problems similar to this: Write an equation of the line that passes throuhg the given point and is parallel to the given line. (4,5),y=x+6. I would muc      Log On


   

Question 120693: i am having trouble solving problems similar to this: Write an equation of the line that passes throuhg the given point and is parallel to the given line.
(4,5),y=x+6. I would much appreciate your help with this problem and an explanation if its not too much trouble.
Thank you
Mike 13y.o.
Found 3 solutions by jim_thompson5910, B-Rod33, nabla:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: Finding the Equation of a Line Parallel or Perpendicular to a Given Line


Since any two parallel lines have the same slope we know the slope of the unknown line is 1 (its from the slope of y=1%2Ax%2B6 which is also 1). Also since the unknown line goes through (4,5), we can find the equation by plugging in this info into the point-slope formula

Point-Slope Formula:

y-y%5B1%5D=m%28x-x%5B1%5D%29 where m is the slope and (x%5B1%5D,y%5B1%5D) is the given point



y-5=1%2A%28x-4%29 Plug in m=1, x%5B1%5D=4, and y%5B1%5D=5



y-5=1%2Ax-%281%29%284%29 Distribute 1



y-5=1%2Ax-4 Multiply



y=1%2Ax-4%2B5Add 5 to both sides to isolate y

y=1%2Ax%2B1 Combine like terms

So the equation of the line that is parallel to y=1%2Ax%2B6 and goes through (4,5) is y=1%2Ax%2B1


So here are the graphs of the equations y=1%2Ax%2B6 and y=1%2Ax%2B1



graph of the given equation y=1%2Ax%2B6 (red) and graph of the line y=1%2Ax%2B1(green) that is parallel to the given graph and goes through (4,5)

Answer by B-Rod33(7) About Me  (Show Source):
You can put this solution on YOUR website!
since it is parallel to y=x+6 it must have the same slope.
therefore the slope equals 1
since it must pass through the point (4,5) you now now a y value and an x value
y=5 and x=4
you then take the general equation of a line y=mx+b and plug in what you know.
y=5, x=4 and m=1
5=4+b
now solve for b
5-4=4-4+b
1=b
now you have your slope and your y-intercept so you can write your equation
y=x+1

Answer by nabla(475) About Me  (Show Source):
You can put this solution on YOUR website!
First, let's take a look at a few examples:
Consider,
A. f%28x%29=3x-2
B. f%28x%29=3x%2B1
Graph of A:
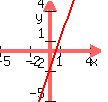
graph%28100%2C100%2C-5%2C5%2C-5%2C5%2C3x-2%29
Graph of B:
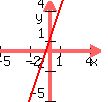
graph%28100%2C100%2C-5%2C5%2C-5%2C5%2C3x%2B1%29
Now, notice how these two lines are parallel when combined into the same graph:
graph%28100%2C100%2C-5%2C5%2C-5%2C5%2C3x-2%2C3x%2B1%29
Notice how y changes per increase in x for each graph. Further, notice that the constants in each equation just shift the line up or down. It shouldn't be surprising, then, that parallel lines have exactly the same slope.
Equation: y=mx%2Bb is the slope-intercept form of a line. m is the slope, b is the intercept.
i.e.: take x=0, y=b implies (0,b) is where the line crosses the y-axis.

So, for the given problem, y=x%2B6, we have m=1 and b=6. If we want to find the equation of a parallel line, m must be the same for the next line!
Now, consider the point-slope form of a line:
y-y%5B1%5D=m%28x-x%5B1%5D%29. The given point in the problem will be our (x1,y1) That is, (4,5).
Then,
y-5=1%28x-4%29
y=x%2B1 is our line.