Question 1203422: Write an equation in slope-intercept form for the line that passes through the given point and is perpendicular to the graph of the given equation. (4, -5), 2x-5y= -10
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Write an equation in slope-intercept form for the line that passes through the given point
and is perpendicular to the graph of the given equation. (4, -5), 2x-5y= -10
~~~~~~~~~~~~~~~~~~~~~~
The given line
2x - 5y = -10
is the same as
y =  .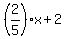
It has the slope  .
A perpendicular line has the slope 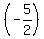 (opposite reciprocal),
so an equation of any perpendicular line is
y = 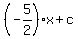 . (1)
Here "c" is some constant, now unknown, which we should determine.
To do it, we substitute coordinates (4,-5) of the given point into equation (1). It gives us
-5 =  ,
or
-5 = -10 + c,
c = 10 - 5 = 5.
So, the final equation of the perpendicular line through (4,-5) is
y =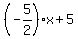 
in slope-intercept form.
Solved.
--------------------
In this site, there is a group of lessons related to this class of problems
- Find the slope of a straight line in a coordinate plane passing through two given points
- Equation for a straight line having a given slope and passing through a given point
- Solving problems related to the slope of a straight line
- Equation for a straight line in a coordinate plane passing through two given points
- Equation for a straight line parallel to a given line and passing through a given point
- Equation for a straight line perpendicular to a given line and passing through a given point (*)
The most relevant to your current problem is the lesson marked (*) in the list.
So start from this lesson.
But if you want to learn the subject in all its aspects, then learn/read all these lessons.
Consider them as your textbook, handbook, tutorials and (free of charge) home teacher.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Answer: y = (-5/2)x + 5
Explanation
2x - 5y = -10 is of the form Ax+By = C, where,
A = 2
B = -5
C = -10
Anything perpendicular to Ax+By = C is of the form Bx-Ay = D
We swap the positions of A and B, then negate one of them.
So all equations perpendicular to 2x-5y = -10 will look like -5x-2y = D.
We can multiply both sides by -1 to get rid of both negative signs on the left hand side, and we end up with 5x+2y = D.
To determine D, we plug in the coordinates (4,-5)
D = 5x+2y
D = 5*4+2(-5)
D = 20 - 10
D = 10
Therefore, the standard form equation perpendicular to the original, and that passes through (4,-5) is 5x+2y = 10
Let's solve that for y to get it into slope-intercept form.
5x+2y = 10
2y = 10-5x
2y = -5x+10
y = (-5x+10)/2
y = (-5x)/2+10/2
y = (-5/2)x+5 which is the final answer.
This is in the form y = mx+b
m = -5/2 = perpendicular slope
b = 5 = y intercept
|
|
|
