|
Question 1202521: The top two dolls that a toy manufacturer makes are called Baby Wiggles and Sleepy Baby.To makes a case of Baby Wiggles takes 5 units of raw material and 1 unit of time to assemble.To make a case pf Sleepy Baby takes 3 units of raw material and 2 units of time to assemble.On a given day the manufacturer has at most 150 units of raw material and 44 units of time.If the manufacturer makes a profit of RM120 on each case of Baby Wiggles and RM100 on each case of Sleepy Baby,how many cases of each type of doll should the manufacturer make in order to maximize profit?
Found 2 solutions by Theo, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = number of cases of baby wiggles.
y = number of cases of sleepy baby.
objective function is profit = 120x + 100y
constraint functions are:
5x + 3y <= 150 for raw material.
1x + 2y <= 44 for units of time.
x >= 0
y >= 0
using the desmos.com calculator at https://www.desmos.com/calculator, you would graph the opposite of the constraint inequalities.
the area of the graph not shaded is your region of feasibility.
the corner points of this region would contain the maximum profit solution.
you would evaluate the objective function at each of these corner points to obtain the maximum profit.
the graph looks like this.
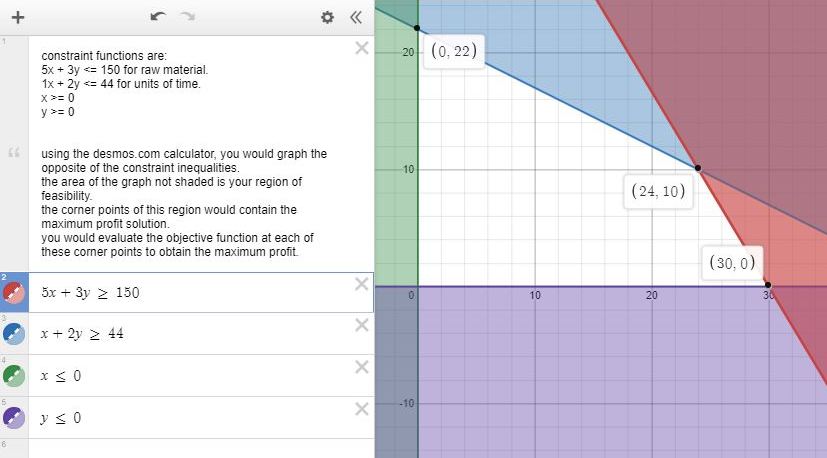
profit = 120x + 100y
at (0,22), profit is equal to 2200
at (24,10), profit is equal to 3880
at (30,0), profit is equal to 3600
maximum profit is at (24,10).
all constraints need to be satisfied at that point.
constraint functions are:
5x + 3y <= 150 for raw material becomes 5*24 + 3 * 3 * 10 = 150.
1x + 2y <= 44 for units of time becomes 24 + 2*10 = 44.
x >= 0 and y >= 0.
all constraints are satisfied.
your solution is 24 cases of baby wiggles and 10 cases of sleepy baby will maximize profit.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Using a graphing calculator to do most of the work for you can get you to the answer faster -- if you know how to use the graphing calculator. But in finding the answer that way you don't get much practice in doing math.
The following is my preferred method for demonstrating to a student the process for solving this kind of problem.
x = # of cases of Baby Wiggles
y = # of cases of Sleepy Baby
The constraints based on availability of raw materials and assembly time are these:


The other two constraints state the obvious fact that the two numbers x and y can't be negative:


Step 1: Graph the constraint boundary lines to determine the feasibility region.
For reasons you will see in a bit, I recommend using slope-intercept form.


The inequalities in this form show that the solutions must lie on or below both constraint boundary lines.
Step 2: Solve the pair of equations for the constraint boundary lines to find their point of intersection and thus determine the corner points of the feasibility region.
I leave it to you to do the relatively easy work to find that the corners are (0,0), (0,22), (24,10), and (30,0).
Step 3: Find the corner point where the profit (objective function) is maximized.
(Note it is NOT necessary, as nearly all references say, to evaluate the objective function at all corners of the feasibility region. That corner point can be determined from the slopes of the objective function and the constraint boundary lines.)
The objective (profit) function is

Put this function in slope-intercept form:

 for some number C for some number C
The profit function will be maximized when a line with slope -6/5 just touches the feasibility region. Since the slope of the objective function, -6/5, is between the slopes of the two constraint boundary lines, the profit function will be maximized at the intersection of the two constraint boundary lines.
So the profit is maximized when x = 24 and y = 10.
ANSWER: The profit is maximum when 24 cases of Baby Wiggles and 10 cases of Sleepy Baby are produced.
CHECK:
corner objective function value, 120x+100y
-----------------------------------------------
(0,0) 0+0= 0
(0,22) 0+2200 = 2200
(24,10) 2880+1000= 3880
(30,0) 3600+0 = 3600
|
|
|
| |