|
Question 1201720: Shade the region defined by this inequality :4y+3x>12
4y+3x>12
y+3x>12/4
y<3-3x
So , I draw y=3-3x and shade the region below the line . The answer on my book is drawn with the area shaded in the upper region .
I chose a point : (0,4) and did substitution : y<3-3x
4<3 ---which is an incorrect statement
Since this point is present in the upper region I shaded the opposite region (below the line ) since the statement is wrong .
So , why is the region shaded in the upper part ? please .
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
The starting inequality is
4y + 3x > 12
We transform it step by step
4y > 12 - 3x
y >  -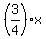 
y > 3 -
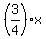The solution set is the half-plane ABOVE the line y = 3 - .
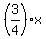The shaded region should show the solution set and must be the UPPER half-plane ABOVE this line.
-------------------
Double check your transformations.
As it is written in your post now, they are incorrect: the last your transformed line is incorrect.
I'm a little surprised how carelessly you do the transformations and don't watch/trace your actions.
Normal procedure is to check, then re-check, then double-check, then cross-check.
If you still have questions, do not hesitate to ask.
///////////////////////
comment from student : Thanks , but since the signs changed (from +3x to -3x) ,
would not the inequality sign change too ? 4y+3x>12 4y < 12 - 3x y<3-(3x/4)
My response : Step by step again, with my comments to each step.
We start from this inequality
4y + 3x > 12 (1)
We are going to move the term 3x from left side of (1) to right side with changing sign
of this term. We do it
4y > 12 - 3x. (2)
This step is the same as to add -3x to both sides of inequality (1).
The sign of the inequality REMAINS THE SAME. It DOES NOT CHANGE at this transformation.
Next we divide inequality (2) by 4.
Since we divide both sides by positive number (4), we DO NOT CHANGE the sign of inequality.
The sign of inequality at this transformation REMAINS THE SAME. We get
y > - 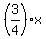. (3)
This inequality (3) is the same as
y > 3 - .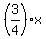
COMPLETED.
The rules are simple.
If you transfer the term from one side inequality to the other side,
you change the sign of this local term, only.
But the sign of inequality remains the same, with no change.
If you divide both sides of an inequality by positive number,
you do it and you DO NOT change the sign of the inequality.
The sign of inequality at such transformation remains the same, with no change.
If you divide both sides of an inequality by negative number,
you do it and you CHANGE the sign of the inequality to the opposite sign.
The sign of inequality at such transformation CHANGES to opposite.
THESE RULES are of ABSOLUTE IMPORTANCE.
THESE RULES are as rigid as steel / (or as a rock).
They work always without any exclusions.
You should ALWAYS follow these rules.
I am glad that you asked this question in your comment, because it should be totally clear.
Your understanding before, as you formulated it in your comment, was incorrect.
Is it totally clear for you now, after my response to your comment ?
-------------------
If you want to get basic knowledge on solving inequalities, look into the lesson
- Solving simple and simplest linear inequalities
in this site.
Consider this lesson as your textbook, handbook, tutorials and (free of charge) home teacher.
Read it attentively and learn how to solve this type of problems once and for all.
\\\\\\\\\\\\\\\\\\\\\\\
comment from student : Now I do understand . Thank you so much !
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Shade the region defined by this inequality :4y+3x>12
4y+3x>12
y+3x>12/4
y<3-3x
So , I draw y=3-3x and shade the region below the line . The answer on my book is drawn with the area shaded in the upper region .
I chose a point : (0,4) and did substitution : y<3-3x
4<3 ---which is an incorrect statement
Since this point is present in the upper region I shaded the opposite region (below the line ) since the statement is wrong .
So , why is the region shaded in the upper part ? please .
First and foremost, why did you divide ONLY the 4y and 12 by 4. What happened to the 3x? Is it not supposed to
be divided by 4 as well?
|
|
|
| |
