SOLUTION: Illustrate a curve that has a line with a point of tangency as well as three other points of intersection. (1 mark)

Might as well let the line be the x-axis.
To have a point of tangency to the x-axis at the origin, 
(i.e., "bounce" off the x-axis there), 
it must have a root or zero at 0 with an even multiplicity, say 2.
So it must have a factor of (x-0)2 or x2

In order for it to intersect (cut through the x-axis) at 1, 2, and 3,
it must have factors (x-1), (x-2), (x-3) of odd multiplicity, say 
multiplicity 1 each. So it must have factors (x-1)1, (x-2)1, and 
(x-3)1, or (x-1), (x-2), and (x-3).

So one such polynomial curve would be





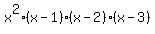
Edwin