Question 1191568: solve -x^3 + 5x^2 - 8x + 4 ≥ 0 algebraically and graphically.
Please provide full answer. Thanks so much for your help :)
Found 3 solutions by Alan3354, math_tutor2020, greenestamps:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! solve -x^3 + 5x^2 - 8x + 4 ≥ 0 algebraically and graphically.
------------------
DL the FREE graph software at
www.padowan.dk (or any graph app)
-----
For padowan:
Use Insert, enter -x^3 + 5x^2 - 8x + 4 and you'll see zeroes at x = 1 and x = 2.
You'll also see that the function is >= 0 for x <= 1, it's = a zero at x = 2.
----------------
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
Graph Approach:
If you typed "graph -x^3 + 5x^2 - 8x + 4" into google without quotes, then it will do as asked.
Though the usual tool I use is GeoGebra. Another handy grapher is Desmos.
There are tons of free options online.
If you prefer your handheld graphing calculator, then of course go for that option.
Whichever graphing tool you use, a cubic curve results which looks like a sort of "S" shape in a sense.
The curve crosses the x axis at x = 1 and x = 2
As the graph shows, when 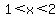 , the curve is below the x axis.
Also, when 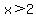 , the curve is below the x axis.
Otherwise, the graph is either on the x axis or above it.
So it's whenever  or when  is when  is the case.
===========================================================================================================
Algebraic Approach:
We'll use the rational root theorem.
Since the first term is either -1 or +1, this means we can look at the plus/minus factors of the last term (4) to generate the list of all possible rational roots.
That list is:
-1, +1, -2, +2, -4, +4
Of course something like +1 is the same as simply 1. I put the plus there to have it pair with its minus counterpart.
From here, we try all of these possible roots one at a time into the expression given.
Let's say we tried x = -1
f(x) = -x^3 + 5x^2 - 8x + 4
f(-1) = -(-1)^3 + 5(-1)^2 - 8(-1) + 4
f(-1) = 18
The result is not zero, so x = -1 is not a root of f(x)
On the other hand, x = 1 is a root because it does lead to f(x) = 0
f(x) = -x^3 + 5x^2 - 8x + 4
f(1) = -(1)^3 + 5(1)^2 - 8(1) + 4
f(1) = 0
If you checked the others, you'd find that only x = 2 is the other root. In fact, it's a double root as the graph previously showed.
This means the cubic factors to -(x-1)(x-2)^2
Once you know the roots are x = 1 and x = 2, you'll set up a number line with those values on it.
Then pick something to the right of x = 1. Let's say we picked x = -1 since we already checked it and found that f(-1) = 18.
This shows that if x < 1, then f(x) > 0
Now pick something between x = 1 and x = 2. Why not x = 1.5
f(x) = -x^3 + 5x^2 - 8x + 4
f(1.5) = -(1.5)^3 + 5(1.5)^2 - 8(1.5) + 4
f(1.5) = -0.125
The result is negative to indicate f(x) is negative on the interval 1 < x < 2, and this matches with what the graph shows.
Lastly, plug in something to the right of x = 2
I'll pick x = 3
f(x) = -x^3 + 5x^2 - 8x + 4
f(3) = -(3)^3 + 5(3)^2 - 8(3) + 4
f(3) = -2
Therefore, f(x) < 0 when x > 2
Putting everything together, we have only true when or when
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
To find where the value of the expression is positive (or negative), we want to find the values for which it is 0.
For an algebraic approach, start with the rational root theorem which tells us the possible rational roots are 1, -1, 2, -2, 4, and -4.
Checking to see if 1 is a root is easy simply by substituting x=1 in the expression. In this example, we quickly see that 1 is a root: -1+5-8+4=0.
x=1 is a root, so (x-1) is a factor of the expression. Reduce the expression to a quadratic by removing the factor of (x-1) using long division or synthetic division.
1 | -1 5 -8 4
| -1 4 -4
+-------------
-1 4 -4 0
The reduced polynomial is
So the completely factored polynomial is
The zeros of the expression are 1 and 2; those are the only values of x where, as you "walk" along the x axis, the value of the function can change from positive to negative or vice versa.
To answer the question, we need to find the values of x for which the value of the expression is 0 or positive.
To do that, we can "walk" along the x axis. The way I find easiest to do that is to start with a "large" positive value of x and walk along the x-axis to the left.
The factored form of the expression is  }.
For "large" values of x (anything greater than the largest root, 2), the signs of the factors are -+++, so the product is negative. So the given inequality is NOT satisfied for large values of x.
Walking left along the x-axis, nothing changes until we reach the largest root, 2. When we pass x=2, the signs of TWO factors change at the same time, so the sign of the expression does not change. The signs of the factors are -+--, so the product is still negative. Since the given inequality is for greater than OR EQUAL TO 0, the inequality is satisfied at the single point x=2.
Continuing our walk to the left, when we pass the next root at x=1, the sign of a single factor changes, so the signs of the factors are now ----, and the product is positive, and the given inequality is satisfied. And x=1 is the smallest root, so the inequality is satisfied for x=1 and for all values of x less than 1.
Our final answer is that the value of the given expression is greater than or equal to zero for  and for the single value x=2.
ANSWER (in interval notation): (-infinity,1] U [2,2]
A graph showing that solution set:
|
|
|
