Question 118380: 3. Sketch the following parabolas. Write whether the roots are real or complex numbers.
a. f(x) = 8x^2 +3
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! From the quadratic formula
the discriminant consists of all of the terms in the square root. So the discriminant is
the discriminant tells us how many solutions (and what type of solutions) we can expect for any quadratic. If the discriminant is greater than zero, then we will have 2 real solutions. If the discriminant is equal to zero, then we will have one real solution. Finally, if the discriminant is less than zero, then we will have 2 imaginary solutions.
So let's use the discriminant to find the number and type of solutions  has:
 Plug in a=8, b=0, c=3
 Square 0 to get 0
 Multiply -4*8*3 to get -96
 Combine 0 and -96 to get -96
Since the discriminant equals -96 (which is less than zero), this means there are two imaginary solutions
Notice if we graph (to graph, just plot a few points), we get
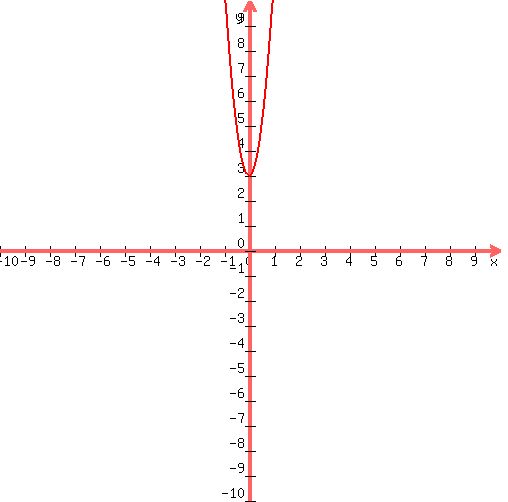
and we can see that the graph does not cross the x-axis, so there are two imaginary solutions.
|
|
|
